KINEMATYKA0013

RUCH JEDNOSTAJNY PROSTOLINIOWY

Zadanie 1.5

składanie ruchów

Prędkość lodzi względem wody w spoczynku wynosi vj.Woda płynie w rzece z prędkością v₂. Jak należy skierować łódź, aby przepłynąć rzekę w kierunku prostopadłym do brzegów? W jakim czasie łódź przepłynie rzekę o szerokości L ? Przedstaw graficznie układ prędkości. Obliczenia numeryczne wykonaj dla v₍ 5 m/s, v₂ = 3 m/s, L - 80 m.

Dane:

= 5 y - prędkość łodzi względem rzeki v₂ = 3 y •• prędkość wody w rzece L = 80 m - szerokość rzeki Szukane:

I = ?    - czas przepływania rzeki

a-?    - kąt pod jakim należy skierować łódź, aby

przepłynęła ona prosto ma drugi brzeg

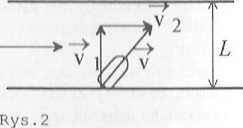
Jeżeli łódź zostanie skierowana prostopadle do brzegu, wtedy prąd rzeki zniesie ją tak, że w rezultacie przybije do przeciwległego brzegu nie w punkcie A, lecz w punkcie B (patrz rysunek 1). Aby łódź wylądowała w punkcie A, należy skierować ją tak, by wypadkowa prędkość (suma wektorowa

prędkości łodzi względem rzeki i prędkości wody w rzece) była prostopadła do brzegów

(patrz rysunek 2). Zgodnie ze wzorem (1.4) prędkość wypadkowa wyniesie: —^    ^ ^

v = vi+v₂.Na rysunku 2 widać, że kąt pomiędzy prostopadłą do brzegów, a kierunkiem wypłynięcia łodzi musi spełniać warunek:

^v2 3

sma = ęq- = -,

czyli kąt pod jakim należy skierować łódź wyniesie:

a » 41

Wyznaczmy z kolei czas l przepływania łodzi przez rzekę. Łódź płynu- ze stałą prędkością,

A

B

Rys. 1

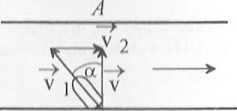
którą możemy wyznaczyć stosując twierdzenie dodawanie prędkości łodzi i rzeki:

Pitagorasa dla trójkąta obrazującego

v7 = v² + v?

| - v -r V₂ ,

skąd otrzymujemy:

_ Z^- 2    2

^v ~ V^v1 ^{— v}2 •

W ruchu jednostajnym czas ruchu znajdujemy korzystając ze wzoru (I 3), czyli w naszym przypadku:

i ostatecznie:

I =

2/,2

I irr/s

m/s

20