Mechanika ogolna0013

20

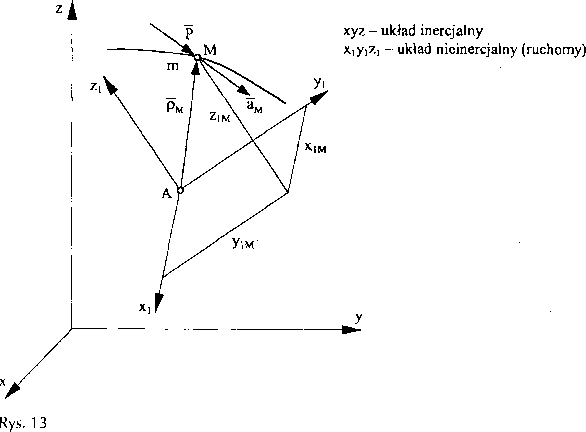
W układzie nieruchomym równanie opisujące ruch punktu materialnego zapisywaliśmy:

m-a_M = P    (63a)

n

gdzie: P =    - geometryczna suma sił zewnętrznych działających na punkt

i=l

materialny, a a_M - wektor przyspieszenia bezwzględnego.

Jeżeli opisujemy ruch punktu względem układu ruchomego, to interesuje nas przyspieszenie względne punktu. Z kinematyki ruchu złożonego punktu wiadomo, że w ruchu złożonym przyspieszenie bezwzględne jest to przyspieszenie określane względem układu nieruchomego. Jest ono sumą trzech składników, z których pierwszy oznacza przyspieszenie unoszenia, drugi przyspieszenie względne (określone względem układu ruchomego), a trzeci oznacza przyspieszenie Coriolisa:

(63b)

((A)

M “ ^aMu ^{+ a}Mw + ^aMcor ~ ^aMb

Podstawiając zależność (63b) do równania (63a), otrzymamy: m-«MH ^V 1 ( '"-“mJ ¹ ('    )

Równanie wektorowe (64) opisuje ruch masy w układzie ruchomym xiy-iZi.

W prowadzamy następujące wektory:

B_u = -m • a_Mu - tzw. siła unoszenia; jest to siła bezwładności,

B_cor = -m ■ a _Mcor - tzw. siła Coriolisa; jest to również siła bezwładności.

<    o do wartości:

B_u = m • a_Mu,

^Bcor ^— ^ ’ ^aMcor ■

<    Matecznie równanie (64) możemy zapisać:

m-a_Mw =P + B_u+B_cor    (65)

'/.r/.uUymy równanie (65) na osie Xiy_xZ\ układu ruchomego. Otrzymamy równania:

^m-*_1M =Px, ^+Bux,

(66)

^1,1 ^IM = ^Py, ^+Buy, ^+Boory,

^m'Z_1M = ^PZ, +^Bu_Zl +^Bco.,

Równania (66) to różniczkowe równania opisujące ruch masy względem układu 11 v i z i, czyli opisuj ące ruch względny masy.

leżeli np.

to równanie (65) przyjmie postać:

"¹!W=P    (⁶⁷)

Wówczas ruch masy w układzie ruchomym lub nieruchomym opisują te same lównnnia.

h/ykłud 7

lliyla pierwsza (rys. 14) obraca się ze stałą prędkością kątową coi wokół nieruchomej osi z. W rowku bryły 1, który nacięto promieniowo, może poruszać się punki. ()pisać zjawisko ruchu bryły 2 względem I. Opory ruchu pominąć.