Mechanika ogolna0005

10

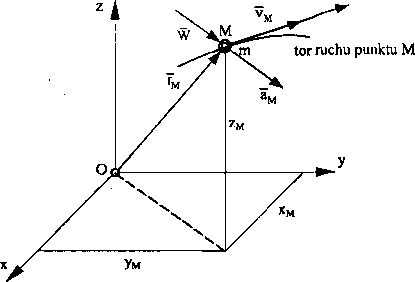
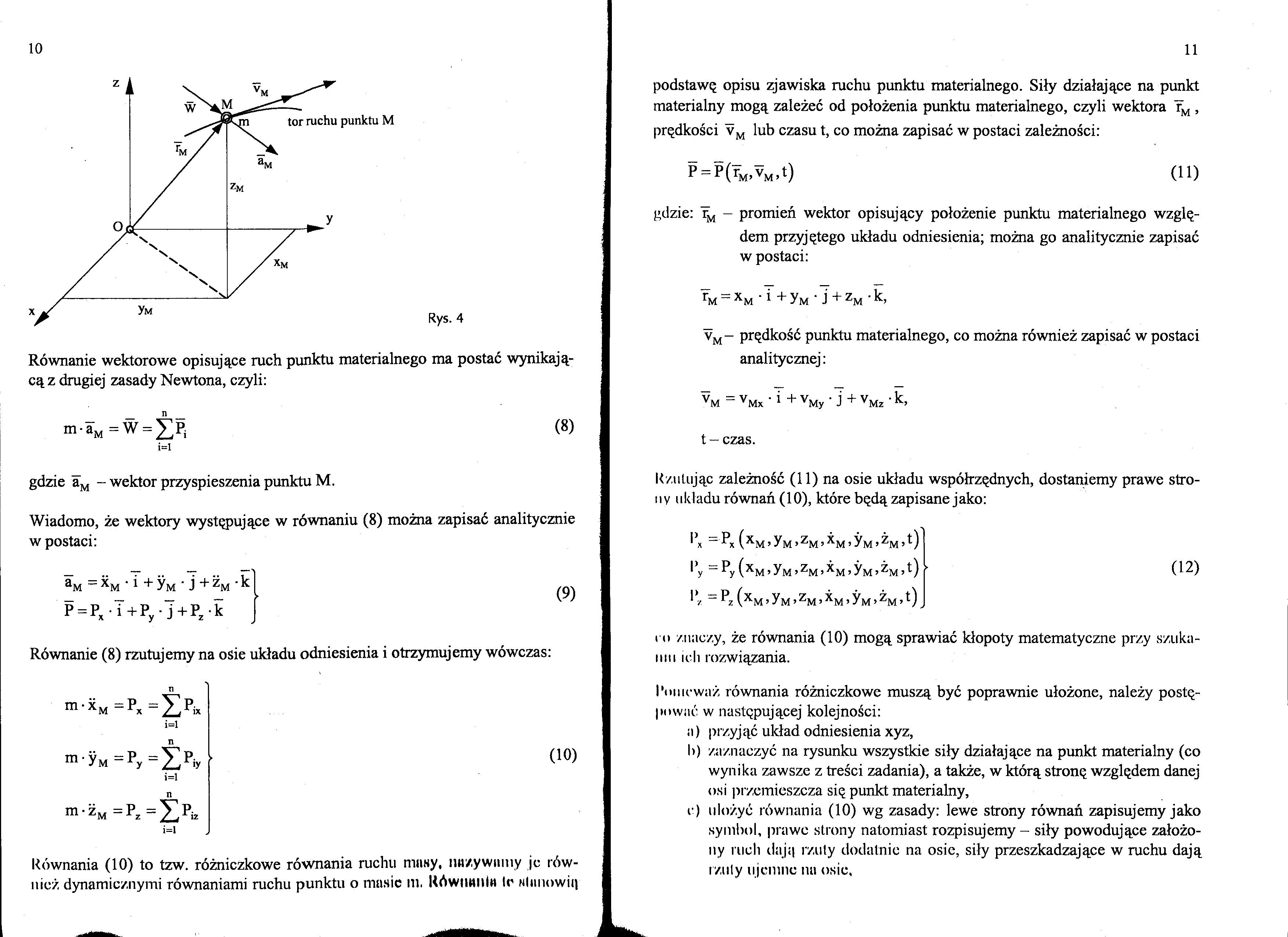
Równanie wektorowe opisujące ruch punktu materialnego ma postać wynikającą z drugiej zasady Newtona, czyli:

m-I_M=W = p    (8)

gdzie a_M - wektor przyspieszenia punktu M.

Wiadomo, że wektory występujące w równaniu (8) można zapisać analitycznie w postaci:

(9)

^aM=*_M-i+y_M-j+ż_M-k P = P_x ■ i + P_y - j + P₂ • k

Równanie (8) rzutujemy na osie układu odniesienia i otrzymujemy wówczas: = ^P* =Z^Pix

i=l

n

(10)

^m-y_M=^Py=2X ■

i=l

^m-ŻM =^pz=ix i=l

Równania (10) to tzw. różniczkowe równania ruchu numy, nazywamy je również dynamicznymi równaniami ruchu punktu o masie m. Równania Ir stanowią podstawą opisu zjawiska ruchu punktu materialnego. Siły działające na punkt materialny mogą zależeć od położenia punktu materialnego, czyli wektora 7_M , prędkości v_M lub czasu t, co można zapisać w postaci zależności:

(11)

gdzie: r_M - promień wektor opisujący położenie punktu materialnego względem przyjętego układu odniesienia; można go analitycznie zapisać w postaci:

r_M = x_M-i+y_M- j+z_M-k,

v_M- prędkość punktu materialnego, co można również zapisać w postaci analitycznej:

V_M^=VMx-^i+VMy-j+VMz-k,

t - czas.

l</litując zależność (11) na osie układu współrzędnych, dostaniemy prawe strony układu równań (10), które będą zapisane jako:

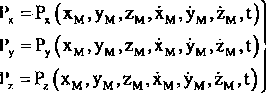
(12)

i o znaczy, że równania (10) mogą sprawiać kłopoty matematyczne przy szukaniu ich rozwiązania.

I'ni ucważ równania różniczkowe muszą być poprawnie ułożone, należy postępować w następującej kolejności:

a)    przyjąć układ odniesienia xyz,

b)    zaznaczyć na rysunku wszystkie siły działające na punkt materialny (co wynika zawsze z treści zadania), a także, w którą stronę wzglądem danej osi przemieszcza się punkt materialny,

c)    ułożyć równania (10) wg zasady: lewe strony równań zapisujemy jako symbol, prawe strony natomiast rozpisujemy - siły powodujące założony ruch dają rzuty dodatnie na osie, siły przeszkadzające w ruchu dają rzuty ujemne nu osie.