Mechanika ogolna0019

38

Równania (79) to rzuty wektora pędu środka masy na poszczególne osie układu odniesienia.

Wektor pędu środka masy układu pokazany na rys. 19 można zapisać jako:

Qs    =Qsx'i + Psy • J + Qsz(80)

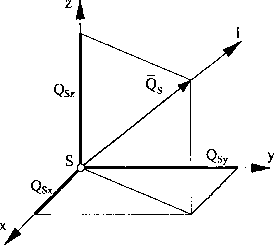
Wartość wektora pędu środka masy wyznaczymy wówczas ze wzoru:

Q_S = >/<&+<&+<&    (⁸¹)

gdzie rzuty wektora pędu na poszczególne osie będą następujące:

n

Qsx

i=l

n

(82)

S

Qs_y^=m-ys=Z^mi^-yi *

i=i

n

Qsz=^m-^ŻS=Z^mi‘^Żi

i=l

W układzie SI jednostką pędu jest

2.4. Równanie ruchu środka masy układu

/lóżniczkujmy równanie (78) względem czasu. Otrzymujemy:

"1 -V_S    '^Vi-

W tównaniu tym -ł _ , co pozwala zapisać je w postaci: v, = a_;

n

m ■ a_s =^m_; -a_;    (83)

i=l

htiiicważ równanie (74) określa, że nij - aj =Pj +Ę, to po wstawieniu tego do w/ni u (83) dostaniemy:

'"■i‘s=Ż^mi-ai=ZPi⁺ŻFi '

i=l    i=l i=l

ii _

Wiklm X^pi jest sumą sił wewnętrznych układu (wzajemnego oddziaływania

i i

(tiMiK Ii'»w materialnych), która wynosi zero. Równanie powyższe będzie miało

"i ■i's=£m_i-a_i=£p_i    (84)

i=l    i=l

/iili /imść (84) to równanie wektorowe opisujące zjawisko ruchu środka masy illdmlii. Wynika z niego, że ruch środka masy całego układu mogą powodować lyllm nily zewnętrzne układu. Siły wewnętrzne mogą zmienić ruch środka masy lytlin części układu, ale nie całości.

M/nlii|i|e wzór (84) na osie układu odniesienia, mamy:

n    n

»> *S -2>i -Xj =£P_ix

il    i=l

n    n

"l y.;    -Yi = X^Piy •

I    I    i-i

II    II

'»X'v*. X¹’.-

l-t    I I

(85)