Mechanika ogolna0046

'M

S;| lo następujące zależności:

n

m * a_s =    - równanie wektorowe opisujące ruch środka masy bryły,

i=l

n

Ks=Zm_s( Pj) - równanie wektorowe opisujące zmianą krętu względem

i=l

środka masy.

Ten układ równań wektorowych zrzutowanych na osie daje sześć różniczkowych równań ruchu. Pierwsze 3 równania wektorowe opisują ruch postępowy środka masy bryły. Następne 3 opisują ruch kulisty względem tego środka.

4. METODY ENERGETYCZNE OPISU ZJAWISKA RUCHU

4.1.    Energia kinetyczna

4.1.1.    Energia kinetyczna punktu materialnego

Punkt o masie m przemieszcza się w układzie xyz (rys. 47), jego energię kinetyczną określimy jako:

E = -jm-v²    (150)

gdzie: m - masa punktu materialnego,

v - prędkość liniowa punktu materialnego.

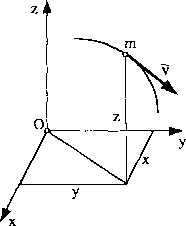
Rys. 47

I uk określoną wielkość nazywamy energią kinetyczną punktu, inaczej energią mclm.

leżeli opisujemy ruch punktu w układzie odniesienia xyz, to prędkość wyrazimy następująco: