Mechanika ogolna0010

20

^m(r_M-cp + 2f_M-⁽p) = £p_i(p=:-P-^sin(p    (43)

i=l

Ponieważ r_M = 1, to r_M ~    % ^_ 0 > m = P/g. Otrzymamy dynamiczne równania

ruchu:

(44)

—l-<p = P-cos(p-N g

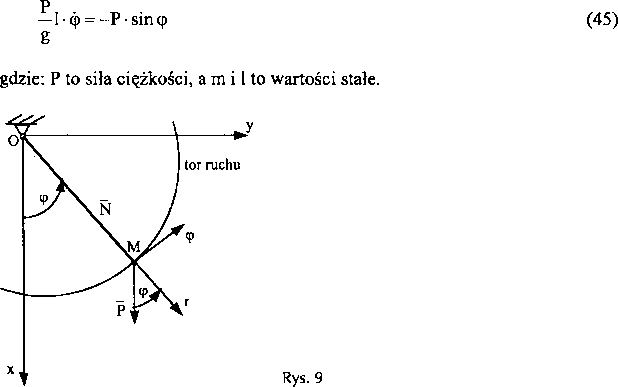
Z równania (45) możemy określić, jak zmienia się kąt 9 w czasie. Rozwiązanie tego równania jest znane wówczas, gdy kąt 9 jest mały. Wtedy sin 9 » 9 i równanie (45) przyjmie postać:

1 ■ 9 + g ■ 9 = 0    (46)

a stąd:

9 + ©o -9 = 0    (47)

gdzie — •—.

Rozwiązanie równania (47) będzie następujące:

<p = Cj • cos co₀ • t + C₂ • sin oo₀ • t    (48)

(j) = -Cj ■ co₀ ■ sinco₀ • t + C₂ • co₀ • cosco₀ ■ t    (49)

Sinic całkowania Cj i C₂ wyznaczymy z równań (48) i (49), znając warunki po-r/.;|lkowe, np.:

ill:i t = t₀ = 0 s, cp = tp₀, (p = <p₀ = 0.

Wprowadzając warunki początkowe do równań (48) i (49), dostaniemy:

Ci ⁼ cpo,

C₂ = 0,

r/.yli ostatecznie otrzymamy:

<p = cp₀ -cosg)₀ • t = (p₀ -cos

Wówczas z równania (44) określimy wartość siły napięcia liny:

P ,

N=P-cosq) 1 - cp =P

g

coscp

g\l

cosę-Jycpo-smyjt

I .(>. Zasada d'Alamberta

Równanie ruchu dla dowolnego punktu o masie m poruszającego się po torze (tys 10) ma postać:

m-a_M=W,

_ 11 _

(jil/K* W P == ^ Pj - wypadkowa sił działających na punkt.

M

rwiiii lównaniu ruchu możemy nadać prostszą postać, przenosząc wszystkie wyiirzy mi jedną stronę. Otrzymamy wówczas:

P l ( m ■ ii_M) 0    (50)