Mechanika ogolna0029

58

(116)

^m-*S=X^Pix

i=l

^m-ys=Ż^Piy

i=l

^m‘Zs = Ż^Pi_Z

i=l

Są to różniczkowe równania ruchu postępowego bryły, czyli dynamiczne równania ruchu postępowego bryły.

3.2. Ruch obrotowy bryły

3.2.1. Dynamika ruchu obrotowego bryły

Kuch obrotowy bryły będzie jednoznacznie określony, jeżeli znamy kąt obrotu (rys. 30), prędkość kątową i przyspieszenie kątowe.

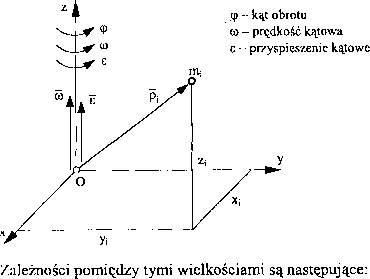
[e = ó) = ćp.

Prędkość i-tego punktu możemy wyrazić jako:

	i	j	k
V, (>> X P,	0	0	w
	■'i	V|

K/uly wektora prędkości na poszczególne osie zapisujemy: v_ix =X; =-©-Yi I

V|y = Yi =co-x_; [•    (117)

V; = Ż; = 0

Mówinmia (117) to tzw. kinematyczne formuły Eulera. Różniczkując je, dostaliśmy rzuty przyspieszenia na poszczególne osie:

(118)

_;ljx=x. =-_£._y. _co²._Xi ii_iy=y_i=E-x_i-G)²-y_i

n _iy. =    = 0

(iKicślamy wektor krętu bryły jako układu punktów względem bieguna O, czyli: K„=K_XJ + K_y-j+K_z-k,

gd/ir rzuty wektora krętu określamy tak jak dla układu punktów materialnych, ii więc:

=Z^mi(yi-^żi-^zi-y_i)⁼-“-Ż^mi-^xi-^zi⁼-^Ix_Z-^co>

i=l    i=l

^K y    ~^xi •^żi)^=c°-Ż^mi -^zi^=_Iy_Z •“>

i=l    i=l

^K/.⁼Ż^mi(^xi-yi-yi-^xi)=®-Ż^mi(^xi +y.²)⁼V®-

i=l    i=l

/tilrżności te zapiszemy dalej w postaci:

K _x = -I_xz • w'

(119)

^lś=-^Iyz-^ft)’

K_Z=I_Z-co

Kównania (119) opisują kręt bryły względem odpowiednich osi układu odnie-Mirma. Jeżeli oś z jest główną osią bezwładności, to I_xz = l_yz = 0, czyli:

K_x 0 K_v 0 K, I, ■«»

(120)