Mechanika ogolna0079

I le/lm Nlopm swobody: s T.l I 5.

I Iklad posiada pięć stopni swobody.

Przykład 25

Rozpatrujemy bryłę sztywną. Obierzmy trzy dowolne punkty mj, m₂, m₃ należące do bryły, nieleżące na jednej prostej (rys. 98). Taki układ trzech punktów modeluje bryłę sztywną.

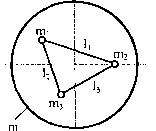
Rys. 98

Ponieważ bryła jest sztywna, to odległości h, 1₂, 1₃ między punktami są stałe. Równania więzów dla bryły:

Fi =(^xi ~^x2)² +(y> -y₂)² +(^z. -z₂)² -1? =°> f₂ =(^xi -^x3)² +(yi -y₃)² +(^zi -z₃)² -i₂ =0, f₃ ~~(^x2 ^X3)² +(y₂-y₃)² +(z₂-Z3)²-i₃ =0.

Mamy trzy punkty należące do bryły, trzy równania więzów, liczba stopni swobody bryły wyniesie:

s = 3-3-3 = 6.

Uwaga!

Stopnie swobody to liczba niezależnych współrzędnych, które w sposób jednoznaczny opisują położenie układu. Każda z tych współrzędnych określa niezależny ruch.

5.4.2. Współrzędne uogólnione

Położenie układów punktów materialnych lub ciał sztywnych będzie jednoznacznie określone, jeżeli podamy współrzędne kartezjańskie wszystkich punk-

Ió\v Iwni/t|t<yt>h llklml Na iikliul imizueiimy więzy <>)'.iimi* zapień mch, czyli nai/iiciuiiy ugnmU/cniu im odpowiednio współrzędne. Wygodnie jcs| opisywać poliiżnnc iikludii za pomooii paitiinclrów, które są już między sobą niezależne Mog;| |o hyc wielkości zupełnie dowolne. Takie wielkości niezależne, wybrane w celu opisania położenia układu punktów lub ciał sztywnych, nazywamy współrzędnymi uogólnionymi.

Przykład 26

Opiszemy ruch wahadła matematycznego (rys. 99).

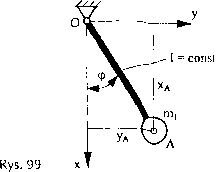
Równania parametryczne punktu A są następujące:

x_A = 1 • cos tp = x_A (cp), y_A =l-sincp = y_A(cp).

Obie te wielkości zależą od kąta obrotu cp, który jest wielkością niezależna Przyjmiemy więc, że: cp = q_x — tzw. współrzędna uogólniona. Będziemy zatem mieli:

^xa ^{= X}A (9l)>

y_A = y_A (<Ti )-Przykład 27

Dwie masy: mi i m₂ zawieszono na nierozciągliwej nici, co pokazano na rys. 100.

Określimy współrzędne punktów charakterystycznych układu. Dla punktu A, w którym zawieszona jest masa ną, mamy:

x_A =1, -coscp, y_A =1, -skicp.