Mechanika ogolna0081

H ('»w 1111111 i i (210) lo l/w. uogólnione przesunięciu wiiliinluo iiklmllL JcnI leli (ylc, ile uklml posiada stopni swobody. l'orówiiuji|c zależności (200) i (210), możemy zapisać:

ST; -- k ■ V|.

W praktyce, aby określić równanie (209), postąpujemy następująco:

Stp^O, 8q₂ =0 ... Sq_s^:=0,

w-fh"

8q₂*0, 8q,=0 ... 8q_s=0,

iul., czyli: 8^ = (SĘ), +(5^ +... + (5Ę)_S.

Przesunięcie wirtualne można zapisać:

(Sm

j=i    j=i

5.4.4. Siły uogólnione

Niech na układ o s stopniach swobody działa układ sił (rys. 102).

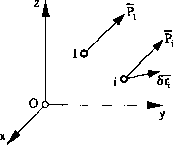
Jeżeli 8q_t ^ 0, Sq₂ =... = 8q_s = 0 (q₂,q₃-.q_s = const. - to wartości stałe), praca przygotowana w przypadku pierwszej współrzędnej uogólnionej (wtedy układ ma 1 stopień swobody) będzie:

SI., I* («.;), +1*2(572), +...+P„(8f„), =ip,(5ri), =ŻP,|?-5q, =

i=l    i=l ^acll

illa drugiej współrzędnej uogólnionej: 8q₂ * 0, 5qj =8q₃ = ... = 8q_s =0, praca przygotowana:

51.2 = P,(S^)_a + ^2(^2)2 ⁺ —+ P„(^)₂ “ŚP.tĄ = !?, J^ą, =

i=l    i=l Wh

= Q₂-5q₂.

Postępując tak z każdą współrzędną uogólnioną, dojdziemy do ostatniej:

8q_s ^ 0,

8q_t =^3 = -=8q_s_, =0,

8L_S = P, (5ij)_s + P₂ (5F,)_S +...+P_n (5f„)_s = £?, (61;)_s = £P, ^-5.,, =

i=l    i=l °4s

=Q_s-8q_s-

Z powyższych zależności określimy wielkości:

Qi-Pf

ti 3q,

(212)

0>=Pf

Qs=ŻPi“

ŚT ' 5q_s

Równania (212) to tzw. siły uogólnione. Jest ich tyle, ile układ posiada stopni swobody.

Uwaga!

Siły uogólnione zastępują działanie tych wszystkich sił występujący eh w układzie, które wykonują pracę wirtualną.