Mechanika ogolna0057

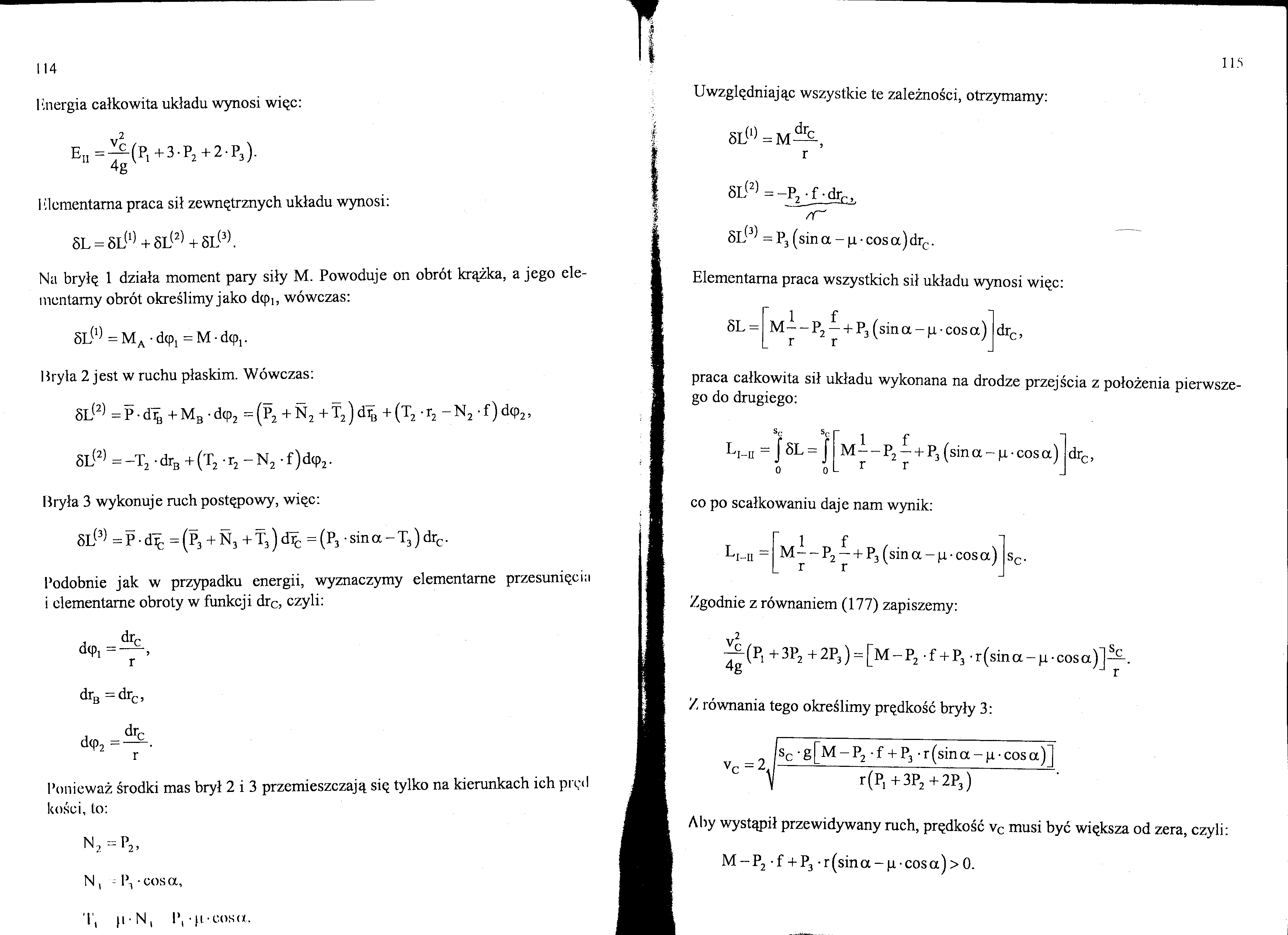
114

linergia całkowita układu wynosi więc:

En=^(P,+3-P₂ + 2P₃).

4g

lilcmentama praca sił zewnętrznych układu wynosi:

8L = 8L⁽¹⁾+8L⁽²⁾+8L⁽³⁾.

Na bryłę 1 działa moment pary siły M. Powoduje on obrót krążka, a jego elementarny obrót określimy jako dep,, wówczas:

Sli¹) = M_a • depj = M ■ depj.

11 ryła 2 j est w ruchu płaskim. Wówczas:

8li ^ = Pd% +M_b -dcp₂ = (P₂ +N₂ + T₂) d% +(T₂ -r₂ — N₂ -f^d^,

8L⁽²⁾=-T₂-dr_B+(T₂-r₂-N₂-f)dcp₂.

Bryła 3 wykonuje ruch postępowy, więc:

5li³) = P-d£ = (P₃ +N₃ + T₃)d£ =(P₃ -sina-T₃)dr_c.

Podobnie jak w przypadku energii, wyznaczymy elementarne przesunięciu i elementarne obroty w funkcji dr_c, czyli:

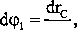
dr_B =dr_c,

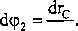
Ponieważ środki mas brył 2 i 3 przemieszczają się tylko na kierunkach ich pręd kości, to:

n₂-p_2>

N, - P, - cos a,

T, ii-N, P,'p-cos«.

8L⁽¹⁾=M^-,

r

8lJ²) = -P^f -dr_r, fC

8li³^ = P₃ (sin a - p • cos a) dr_c.

Elementarna praca wszystkich sił układu wynosi więc:

8L =

1 f

M—P₂ — + P₃ (sin a - p • cos a)

dr_c,

praca całkowita sił układu wykonana na drodze przejścia z położenia pierwszego do drugiego:

L_WI = / 6Ł = /

0 0

co po scałkowaniu daje nam wynik: ^1-11 =

“ i    f

M—P₂ — + P₃(sina-p-cosa) r    r

1    f

M— P₂ — + P₃ (sin a - p • cosa) r    r

Sr-

dm

Zgodnie z równaniem (177) zapiszemy:

2

^-(Pj +3P₂ +2P₃) = [M-P₂ -f + P₃ -r(sina-p-cosa)]~.

Z równania tego określimy prędkość bryły 3:

s_c-g[M-P₂-f+ P₃ ■r(sinoc-p-cosa)]

^{VC =} 1    ^r(P, +3P₂ +2P₃)    '

Aby wystąpił przewidywany ruch, prędkość v_c musi być większa od zera, czyli: M-P₂-f + P₃r(sina-pcosa)>0.