Mechanika ogolna0066

132

gdzie: 57 - tzw. wektor przesunięcia przygotowanego (albo wirtualnego), v - tzw. wektor prędkości możliwej (prędkości zgodnej z więzami),

X - współczynnik proporcjonalności, który przyjmujemy np. X = 1.

Równanie (194) to tzw. wektor przesunięcia przygotowanego (możliwego), jest on proporcjonalny do wektora prędkości możliwej. Gdy ruch opisujemy w układzie xyz, to:

(195)

5r = 5x ■ i + 8y■j + 8z•k

Wyrażenie:

8L = P ■ 57 = P_x • 8x + P_y ■ 5y + P_z ■ 5z = P • 5r • cosa    (196)

jest to tzw. praca przygotowana (lub praca wirtualna) wykonana przez siłę lub układ sił.

Załóżmy, że na układ narzucone są więzy idealnie gładkie (beztarciowe, wówczas reakcje więzów są tylko reakcjami normalnymi). Jeżeli punkt, na który działają siły, pozostaje w równowadze statycznej, to:

P + R = 0,

gdzie: P - wektor sił czynnych,

R - wektor sił reakcji.

Praca wirtualna sił czynnych i reakcji takiego układu wynosi zero:

8L = (P + R.)87 = P ■ 87 + R • 87 = 0.

Reakcje więzów nie wykonują pracy, bo reakcje są tylko normalne, czyli:

R • 87 = 0.

Możemy więc zapisać, że:

5L = P • 57 = 0    (19/)

Zależność (197) jest to tzw. zasada prac przygotowanych (lub wirtualnych). Z równania tego wynika, że punkt będzie pozostawał w równowadze slatye/,ur|, jeżeli praca przygotowana wykonana przez wszystkie siły czynne dzialajnec im punkt będzie równa zeru! Opisując ruch w układzie xyz, równanie (197) znpl szumy jako:

8L = P-8T=P_X • 8x + P_y • Sy + P_z • 8z = O    (198)

Jeżeli występuje układ sił działających na bryłę lub układ brył, to zasadę prac przygotowanych określimy wówczas jako:

5L =    • 57j = £(^pix ■ 5Xj + P_iy ■ 8y_; + P_iz ■ 8_Zj) = 0    (199)

i=l    i-1

Wzór (199) jest to zasada prac przygotowanych dla złożonego układu sił. Równanie to pozwala na szukanie położenia równowagi statycznej dowolnego układu sił.

5.1.2. Praca przygotowana układu sił działających na bryłę w ruchu postępowym

W ruchu postępowym (rys. 76) mamy: 8ij = 8r_s,

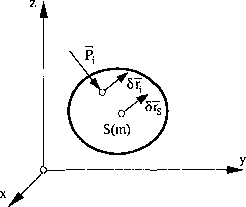
wówczas pracę przygotowaną w ruchu postępowym opisuje zależność:

(200)

8L = P-8% =P_X • 8x_s + P_y • 8y_s + P_z • 8z_s = 0

gdzie: P = ^P_; - wektor wypadkowy sił działających na bryłę,

i=l

8% = X ■ v_s - wektor przesunięcia przygotowanego środka masy.

Równanie (200) określa równowagę statyczną układu sił działających na bryłę W ruchu postępowym.