Mechanika ogolna0061

122

Płaszczyzna xy jest tzw. płaszczyzną porównawczą. Zakładamy, że potencjał na tej płaszczyźnie jest zerowy. Praca sił pola potencjalnego przy przejściu z punktu A do B będzie wynosić:

^LAB =^VA -^VB =^m-g'^ZA    =m-g(^ZA-^ZB) ^{= m}-g-^h = ^m-g'^ZA-

Pole potencjalne sprężyny - siła reakcji sprężyny zależy od deformacji sprężyny. Jeżeli założymy liniową zmianę siły reakcji sprężyny, to jej wartość będzie następująca:

S = k-x[N],

gdzie: k- tzw. współczynnik sprężystości, wyznaczany na drodze doświad-

N

czalnej

x - zmiana długości sprężyny w porównaniu z długością początkową sprężyny, czyli deformacja sprężyny [m].

Zakładamy, że ściskamy sprężynę o x, jak pokazano na rys. 71.

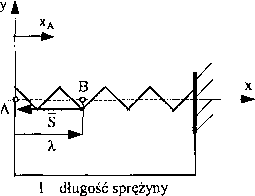
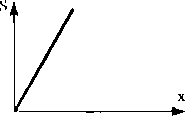
Rys. 71

Zgodnie z rys. 71 siła reakcji sprężyny daje rzuty na osie:

P_x = -S = -k • x,

l’_v 0,

I- 0.

Ponieważ równania (188) są spełnione, to szukamy potencjału pola sprężyny z zależności:

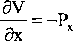
j*5V = Jk • x ■ dx, czyli:

V    =—k-x² +G

2

Wyznaczymy stałą całkowania. Zakładamy, że gdy x = 0, V = 0, czyli C = 0. Ostatecznie potencjał pola sprężyny określimy jako:

V    = ^k-x²    (191)

1 2

Jeżeli V = —k■ x =const.,to x-±const. - mamy równanie powierzchni ekwipotencj alnej.

Praca sił pola potencjalnego sprężyny przy przejściu z punktu A do B będzie wynosić:

Lab = V_A -V_B = |k-xi -|k-x² =i_k(x^ -x² ) = -ik-x² = ~k-Z²

(192)

gdzie X - wartość bezwzględna zmiany długości sprężyny.

Równowaga w polu potencjalnym

Jeżeli w polu potencjalnym punkt materialny ma pozostać w równowadze statycznej, to oczywiście siła działająca w tym punkcie jest zerem, czyli P_x, P_y i P_z = 0. Wtedy z równań (186) wynika, że:

= 0, jest to równanie dodatkowe w tych punktach, gdzie

występują minima lub maksima potencjału. Punkt, w którym występują ekstremu potencjału to jego położenia równowagi statycznej.

W polu potencjalnym punkt, w którym potencjał osiąga minimum jest położeniem równowagi stałej, jest to tzw. twierdzenie Dirichlcln.