Mechanika ogolna0011

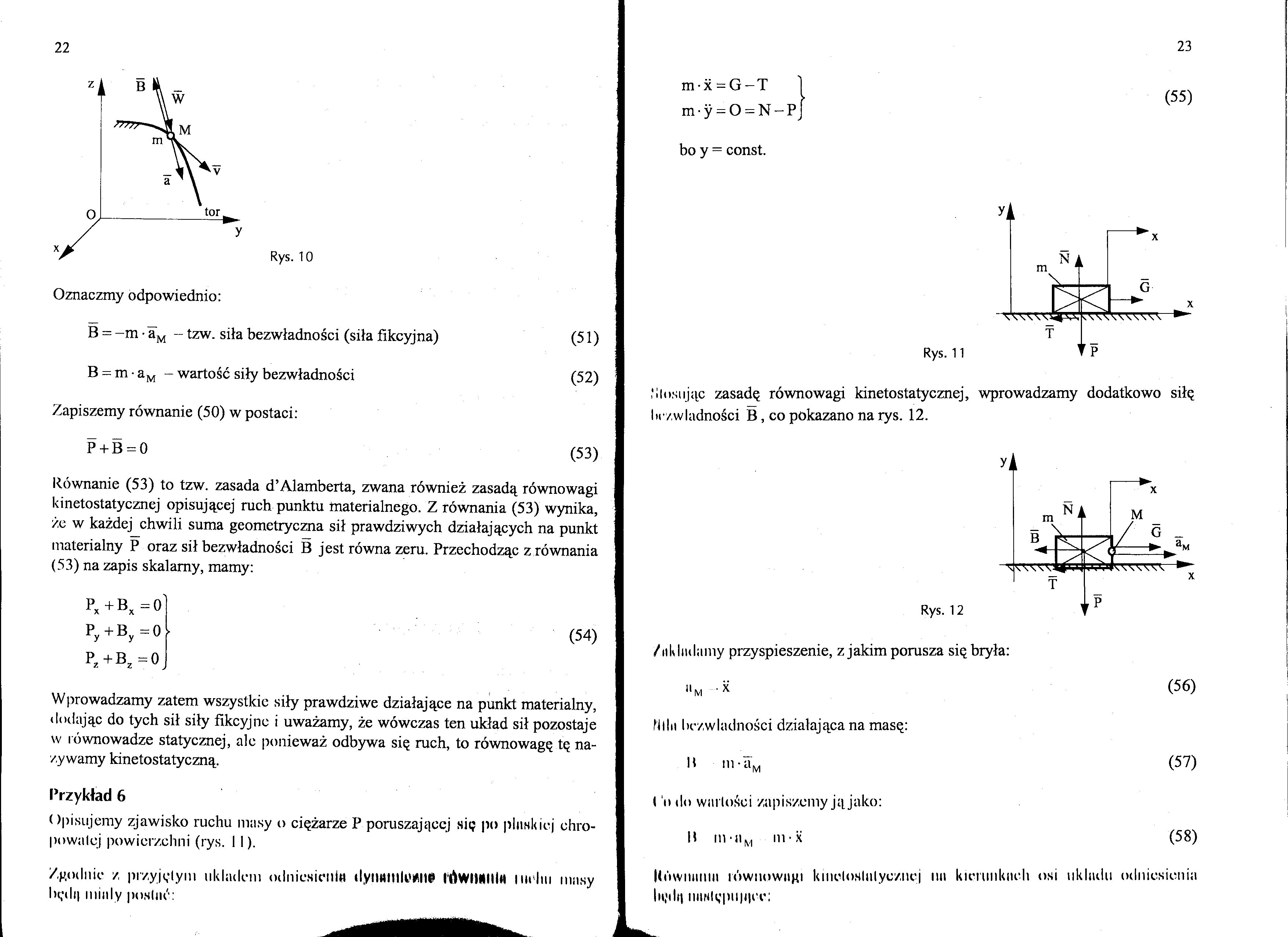
22

Oznaczmy odpowiednio:

B = -m • a_M - tzw. siła bezwładności (siła fikcyjna)    (51)

B = m • a_M - wartość siły bezwładności    (52)

Zapiszemy równanie (50) w postaci:

P + B = 0    (53)

Równanie (53) to tzw. zasada d’Alamberta, zwana również zasadą równowagi kinetostatycznej opisującej ruch punktu materialnego. Z równania (53) wynika, że w każdej chwili suma geometryczna sił prawdziwych działających na punkt materialny P oraz sił bezwładności B jest równa zeru. Przechodząc z równania (53) na zapis skalamy, mamy:

P_x+B_x=0

(54)

P_y+By=0 •

^PZ^+BZ=0.

Wprowadzamy zatem wszystkie siły prawdziwe działające na punkt materialny, dodając do tych sił siły fikcyjne i uważamy, że wówczas ten układ sił pozostaje w równowadze statycznej, ale ponieważ odbywa się ruch, to równowagę tę nazywamy kinetostatyczną.

Przykład 6

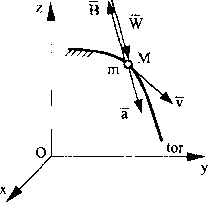
Opisujemy zjawisko ruchu masy o ciężarze P poruszającej się po pińskiej chropowatej powierzchni (rys. I I).

/godnie z przyjętym układem odniesieniu ilyitMItlllMHt ińWIWIIiH linlui masy będą miały postać:

mx=G-T _m.y = 0 = N-P

bo y = const.

Rys. 11

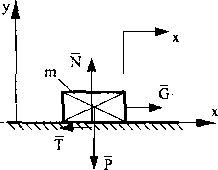
i losując zasadę równowagi kinetostatycznej, wprowadzamy dodatkowo siłę bezwładności B, co pokazano na rys. 12.

Rys. 12

(56)

(57)

Zakładamy przyspieszenie, z jakim porusza się bryła: «m ■*

Nilu bezwładności działająca na masę:

B m-a_M

I u do warlości zapiszemy ją jako: (58)

Mównamn równowagi kineloslulyezncj na kieninkaeli osi układu odniesienia liętlą naslępiipice;