0000061 (6)

gdzie:

8tl²/c

przy czym J = O, 1,2, ... oznacza odpowiednią liczbę kwantową, I — moment bezwładności cząsteczki, c — prędkość światła. Dla przykładu, przejściu ze stanu 7=3 do stanu 7=4 odpowiada różnica energii &£_rol =8 B c h. Dla cząsteczki HC1 ta różnica energii wynosi około 0,01 eV, do wzbudzenia tego poziomu należałoby więc użyć kwantu o energii = 0,01 eV, co odpowiadałoby długości fali około 124 jam, a więc w dalekim zakresie podczerwieni.

Widma rotacyjne leżą w dalekiej podczerwieni oraz w zakresie mikrofal (100-1000 (im), ich badanie dostarcza cennych informacji o budowie cząsteczki. Można znaleźć jej moment bezwładności, a co za tym idzie, odległości międzyatomowe w cząsteczce, np. dla HC1 otrzymuje się odległość między atomami 0,128 nm.

Energia oscylacyjna jest związana z drganiami atomów cząsteczki względem siebie. W najprostszym przypadku cząsteczki dwuatomowej można sobie ją wyobrazić jako dwie kulki związane sprężyną. Atomy wykonują wtedy ruch harmoniczny. Energia takiego ruchu jest według mechaniki kwantowej skwantowana i wyraża się wzorem

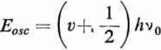
gdzie t? = 0,1, 2, ... są oscylacyjnymi liczbami kwantowymi, v₀ — częstotliwość drgań oscylatora. Energia wzbudzenia, potrzebna do przejścia z poziomu energetycznego v = 0 na poziom v = 1, wynosi AjE_osc = /;v₀. Energia wzbudzenia poziomów oscylacyjnych jest rzędu 10^_1 eV, odpowiada jej długość fali rzędu 10 (im, a więc bliższej podczerwieni. Wzór 2.3 należy uważać za przybliżenie, gdyż drgania atomów w cząsteczce nie są harmoniczne. Cząsteczki niepolarne, jak H₂, O, itp. nie dają widm oscylacyjnych (odnosi się to także do rotacyjnych), gdyż drgania atomów w tego rodzaju cząsteczkach nie dają zmian momentu dipolowego, co jest koniecznym warunkiem emisji promieniowania elektromagnetycznego. W związku z tym powietrze nie absorbuje promieni podczerwonych Słońca, natomiast pochłania je w pewnych zakresach widma para wodna. Na energie oscylacyjne nakładają się zawsze rotacyjne, mamy więc w zasadzie do czynienia z widmami oscylacyjno-rotacyjnymi, w dziedzinie podczerwieni. Poziomy oscylacyjno--rotacyjne przedstawia ryc. 2.8. Widma oscylacyjno-rotacyjne dostarczają ważnych informacji o strukturze cząsteczek. Niektóre częstości są charakterystyczne dla określonych grup atomów, np. grupie C-H odpowiada liczba falowa około 2900 cm^-1, nawet gdy wchodzi w skład innej cząsteczki można ją z widma rozpoznać.

Energia elektronowa cząsteczki związana jest z elektronowymi poziomami molekuły. Przejście elektronów na wyższe poziomy energetyczne jest możliwe przy energiach kwantów w zakresie światła widzialnego czy nawet nadfioletu. W cząsteczce stan elektronu jest także opisany czterema liczbami kwantowymi n, l, X, m_s, znaczenie tych liczb jest takie samo jak w atomie, z tym że odpowiednikiem orbitalnej liczby magnetycznej m, jest w cząsteczce liczba X. Na wzbudzone stany elektronowe nakładają się wzbudzone stany oscylacyjne i rotacyjne zgodnie z wzorem 2.1. W ten sposób powstaje bardzo złożone widmo pasmowe elektronowo-oscylacyjno-rotacyjne; odpowiednie poziomy

5* 67