MG!80

przy czym e oznacza tutaj odkształcenie liniowe przekątnych kostki pierwszej. Mierząc to odkształcenie można obliczyć kąt y odkształcenia posta. ciowego.

Na podstawie rys. 4.15 można stwierdzić, że stan czystego ścinania zachodzi wtedy, gdy w badanym elemencie odkształcenia liniowe dwóch wzajemnie prostopadłych odcinków są sobie równe co do wartości, a różnią się znakami.

Stan taki istnieje np. przy skręcaniu rur cienkościennych o dowolnym obrysie. Za profil cienkościenny uważa się taki, w którym stosunek grubości ścianki profilu do innego wymiaru charakteryzującego przekrój jest dużo mniejszy od jedności. Na rys. 4.16 przedstawiono schematycznie taki profil. Kształt profilu jest opisany promieniem wodzącym r = r(a), liczonym do linii środkowej ścianek profilu; grubość ścianek może być też funkcją kąta a tzn. ó = ó(a).

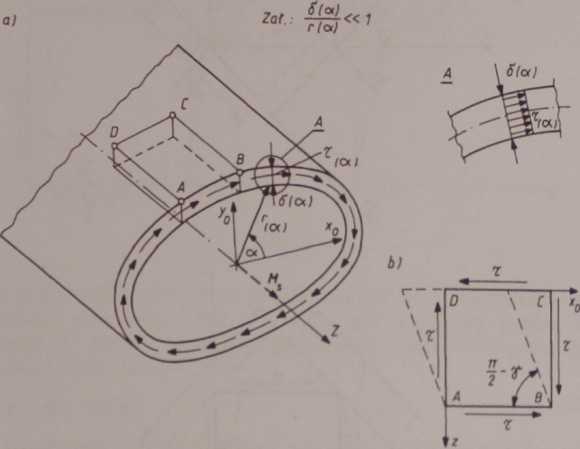
Rys. 4.16

Przyjmuje się z techniczną dokładnością, że naprężenia styczne t wywołane momentem skręcającym M_t są stałe na grubości ścianki. Można dowieść, że wyznacza się je ze wzoru Bredta [4], a mianowicie

t_b =-— [MPa],    (4.62)

²V«

gdzie:

S, — pole przekroju profilu ograniczone linią środkową Ścianek.

Kijanki 6. Gdy z takiego profilu wytnie się nieskończenie mały element W^cln określony liniami prostopadłymi i równoległymi do osi rury ^ą\6ą), to element ten będzie obciążony, co pokazano na rys. 4.16b. Wy-(iy^s‘ _z warunków równowagi tego elementu. Jest więc on poddany czyste-

ścinaniu i odkształci się tak, jak to na rys. 4.16b zaznaczono liniami prze-Jeżeli więc na taki element naklei się dwa tensometry pod kątem

stąd

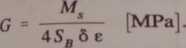
(4.64)

Wzór ten jest podstawą doświadczalnej metody wyznaczania modułu Kirchhoffa.

4.3.2. Analiza doświadczalna

Stanowisko laboratoryjne składa się z cienkościennej rury kołowej o stałej grubości ścianki Ó, zamkniętej sztywnymi wręgami (rys. 4.17). Do wręg tych przyłożone zostają momenty zewnętrzne skręcające rurę. Momenty te zamieniają się na obwodzie rury w równomiernie rozłożone naprężenia styczne. Średnia średnica rury wynosi D =2 R ; jest znany moduł Younga E i współczynnik Poissona v materiału rury. Moment skręcający M_a jest realizowany przez zawieszenie na ramieniu r odpowiedniego ciężaru Q, czyli

(4.65)

(4.66)

M_s = Qr [N - mm].

Pole S_B we wzorze (4.64) przyjmuje wartość S_fl = n R² [mm²].

Stąd wzór na moduł Kirchhoffa uzyskuje końcową postać (4.67)

gdzie:

121