Mechanika ogolna0042

X4

Wzór (149) jest to tzw. twierdzenie Resala, opisujące ruch kulisty będący precesją regularną. W równaniu tym u_A, zgodnie z iloczynem wektorowym, jest wektorem prędkości końca wektora krętu K₀ i jest równy sumie wszystkich sił zewnętrznych działających na bryłę.

Przykład 12

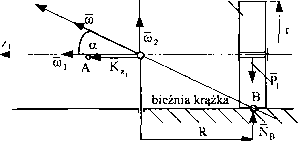
()kreślić reakcję podłoża działającą na krążek toczący się po powierzchni jak na rys. 41.

fi

z

krążek

M

r

R

Kys. 41

Dane:

P, P - siła ciężkości działająca na bryłę [N],

co₂ = const. - prędkość kątowa prece-rad

sji — ,

s

odpowiednie wielkości geome

tryczne [m].

Szukamy prędkości kątowej obrotu własnego. Aby ją znaleźć, musimy określić położenie chwilowej osi obrotu. Oś chwilowa zawiera punkty, których prędkość liniowa w danej chwili wynosi 0. Jeden taki punkt to środek ruchu kulistego O, drugi to punkt B zetknięcia krążka z nieruchomym podłożem. Na osi tej leży wektor prędkości kątowej ro . Przyjmijmy punkt O za początek nieruchomego układu współrzędnych xyz oraz ruchomego układu odniesienia x₁y₁Zi. Oś z przyjmujemy tak, aby kierunek prędkości ćo₂ pokrywał się z kierunkiem osi z. ()ś z, układu ruchomego jest osią obrotu własnego bryły. Prędkość kątowa obro-lu własnego jest składową prędkości bezwzględnej. Jej wartość znajdziemy z warunku:

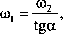
gdzie:

r

iv.yli:

R

CO; =—co₂=const.

Zgodnie z uproszczoną teorią ruchu kulistego kręt krążka wzglądem środka ruchu kulistego będzie wynosił:

K₀=K_Zi=I_2i-dV

Pochodna krętu po czasie zgodnie ze wzorem (149) jest równa:

K₀=K,_i=u_A=S₂xK_2i=XMo(Pi).

i-1

gilzie:

^u _A - ®2 ' K₂j • sin^“J = N_b ■ R - P, • R.

I Iw/ględniając wartość wektora krętu, otrzymamy:

N_b =^Pi+Iz₁ '®r®2 >

pu;d kość obrotu własnego (Oj =—<x>₂, co po podstawieniu do podanego wcze-r

uii u-j wzoru da:

N|! ⁼ ?1 + I_z, “®2-

les! lo wartość siły nacisku w punkcie B. Widzimy, że wartość ta w dużej mie-i/c zależy od prędkości kątowej precesji co₂. Zjawisko to jest wykorzystywane lip w młynach walcowych do zwiększania siły nacisku walca na rozdrabniany miilci ial.

I Iw.iga!

Jeżeli bryła obraca się wokół własnej osi symetrii, a oś ta zmienia swoje położenie w czasie, lo wówczas bryłę nazywamy żyroskopem. Analizując ruch żyroskopu, mówimy o wyNlępowiimu Izw. deklu żyroskopowego.