Mechanika ogolna0021

(90)

to wówczas:

m--m- Vs⁰⁾ =0,

czyli:

m • v_s = Q_s = const.

Zależność (90) jest to tzw. zasada zachowania pędu układu punktów materialnych. Rzutując wzór (90) na osie układu odniesienia, dostaniemy:

(91)

m ■ x_s = Q_x = const. m-y_s=Qx = const. ■ m ■ ż_s = Q_x = const.

Z równania (90) wynika, że wektor prędkości środka masy układu jest wówczas stały co do kierunku i wartości.

TEMAT 3

Wykorzystując równania opisujące zjawisko ruchu układów punktów materialnych, określić:

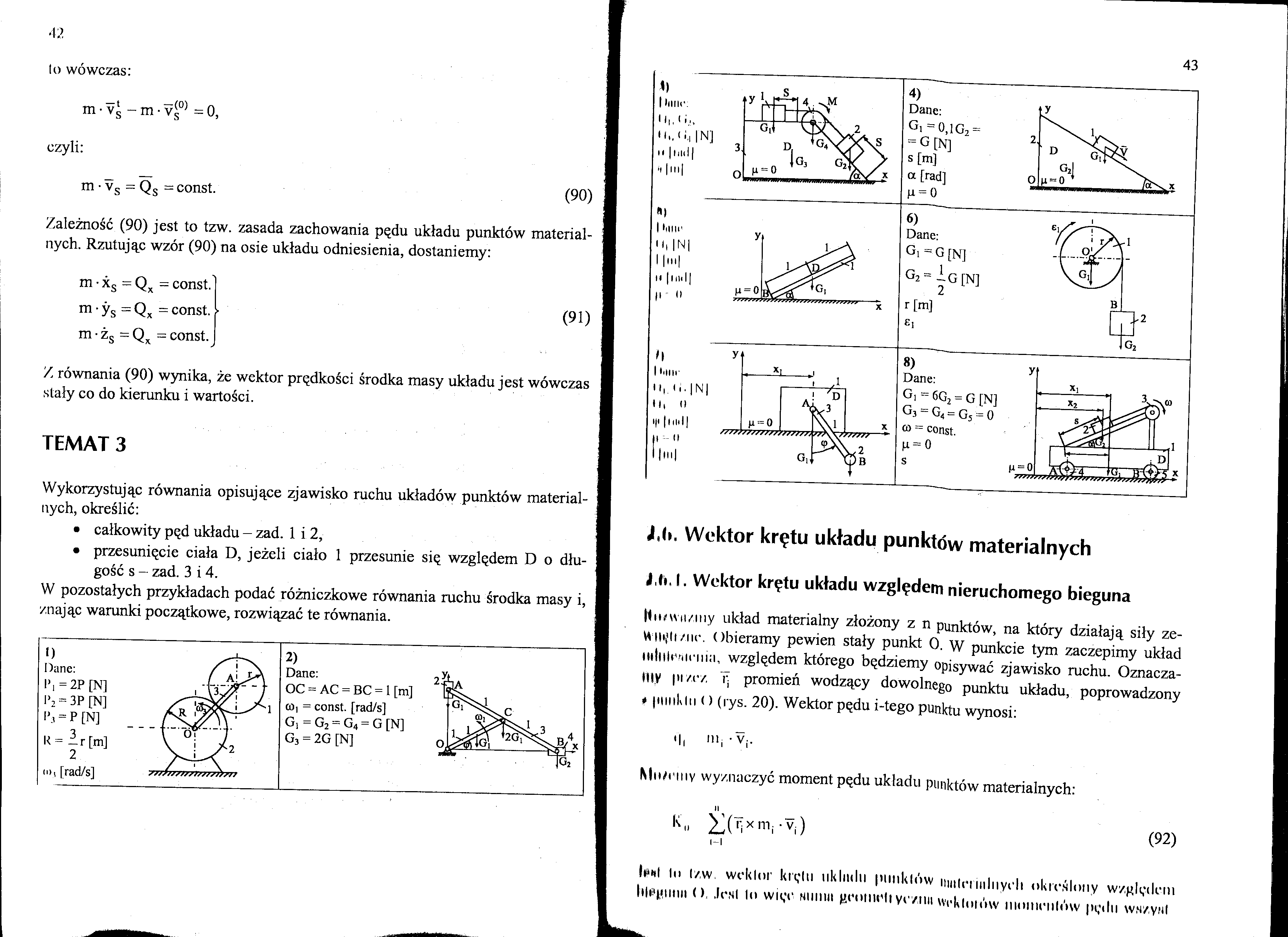
•    całkowity pęd układu - zad. 1 i 2,

•    przesunięcie ciała D, jeżeli ciało 1 przesunie się względem D o długość s - zad. 3 i 4.

W pozostałych przykładach podać różniczkowe równania ruchu środka masy i, znając warunki początkowe, rozwiązać te równania.

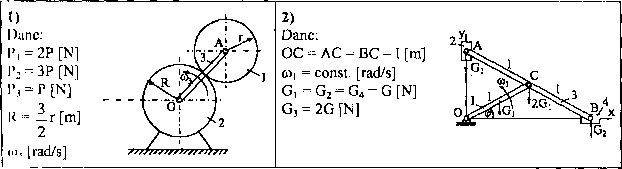
J,(t. Wektor krętu układu punktów materialnych

|,f». I. Wektor krętu układu względem nieruchomego bieguna

Hnmuzmy układ materialny złożony z n punktów, na który działają siły ze-Wiujlt.mu'. Obieramy pewien stały punkt 0. w punkcie tym zaczepimy układ Millłirnu-ma, względem którego będziemy opisywać zjawisko ruchu. Oznaczamy pi/rz i-j promień wodzący dowolnego punktu układu, poprowadzony * (ttmklu <) (rys. 20). Wektor pędu i-tego punktu wynosi:

Mi »VVj.

Mn/einy wyznaczyć moment pędu układu punktów materialnych:

(92)

K., X(^ri^xm>"^vi)

L

(pil In l/w, wcklor kręlti układu punktów itmlrnnlnyelt określony względem lij^gunn O. Jrsl In więc niiiiui geomeliyc/iiu wrklmów momenlów pędu wszyul