Mechanika ogolna0084

fł.4.(». Pole |Milem J(ilne

Jeżeli w naszym układzie pracę wykonują tylko siły pola potencjalnego, lo wówczas zapiszemy, że potencjał jest funkcją współrzędnych uogólnionych, czyli:

(21 S)

V = V(q₁,q₂...q_s)

Określając pochodne cząstkowe potencjału V, opierając się na współrzędnych uogólnionych, dostaniemy:

av

5q,

Qi =“

q₂ =

dV

dą₂

(2U»)

Q_S

av

3q_s

Z równania tego wynika, że uogólnione cząstkowe pochodne względem odpowiednich współrzędnych uogólnionych określają siłę uogólnioną.

Przykład 30

Dla układu płaskiego pokazanego na rys. 105 określić siły uogólnione.

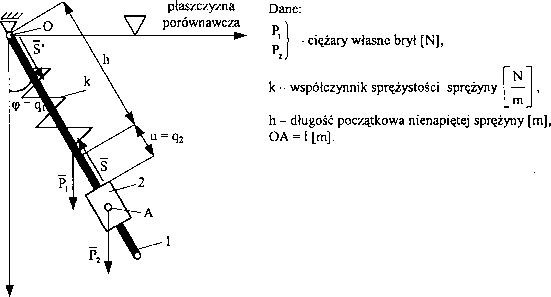
Rys. 105

Wahadło może się obracać wokół punktu O, suwak 2 może przemieszczać się po wahadle. IJklad posiada więc dwa stopnie swobody. Przyjmijmy pierwszą współrzędną uogólnioną: kąt obrotu bryły 1 (qi = ęp), drugą współrzędną: przemieszczenie wodzika 2 względem 1 (q₂ = u). Potencjał układu jest równy sumie potencjału grawitacyjnego i sprężystego:

V(q₁,q₂)-

V = -mj -g-^-cos(p-m₂ -g(h + u)cos(p + ^-k-u¹

Zgodnie z równaniem (213) siły uogólnione wynoszą:

„ dV    1 .    /,    \ .

Qi =-— = -111, -g—•sin(p-m₂ -g^h + ujsincp,

Scpj    2

_n dV    .

Q₂ =--= m₂ • g • coscp -k• u,

du

Szukamy położenia równowagi statycznej układu. Równowaga ta wystąpi wówczas, gdy spełnione jest równanie (211), tzn.:

Qi =-m! -g—sin(p₀ -m₂ -g(h + u₀)sincp₀ =0, Q₂ =m₂ - g-cosepo -k-u₀ =0,

gdzie: (p₀ - kąt, przy którym występuje równowaga statyczna,

u₀ - statyczna deformacja sprężyny (odkształcenie sprężyny w położeniu statycznym),

ną-g = Pi - siła ciężkości bryły 1, m₂-g = P₂ - siła ciężkości bryły 2.

Uwzględniając powyższe zależności, zapiszemy, że:

(1)

Pi_ ₊ P₂(_{h + Uo})

sincp₀ =0,

1

P₂-coscpo-k-u₀ =0.

Równanie (1) jest spełnione, gdy sincp₀ = 0, czyli: cp₀ = 0,7t, 2 ■ n,.... Aby ustalić, które rozwiązanie jest prawdziwe, wykorzystajmy twierdzenie mówiące, że położenie równowagi w polu potencjalnym jest tam, gdzie potencjał osiąga minimum, czyli: