Mechanika ogolna0053

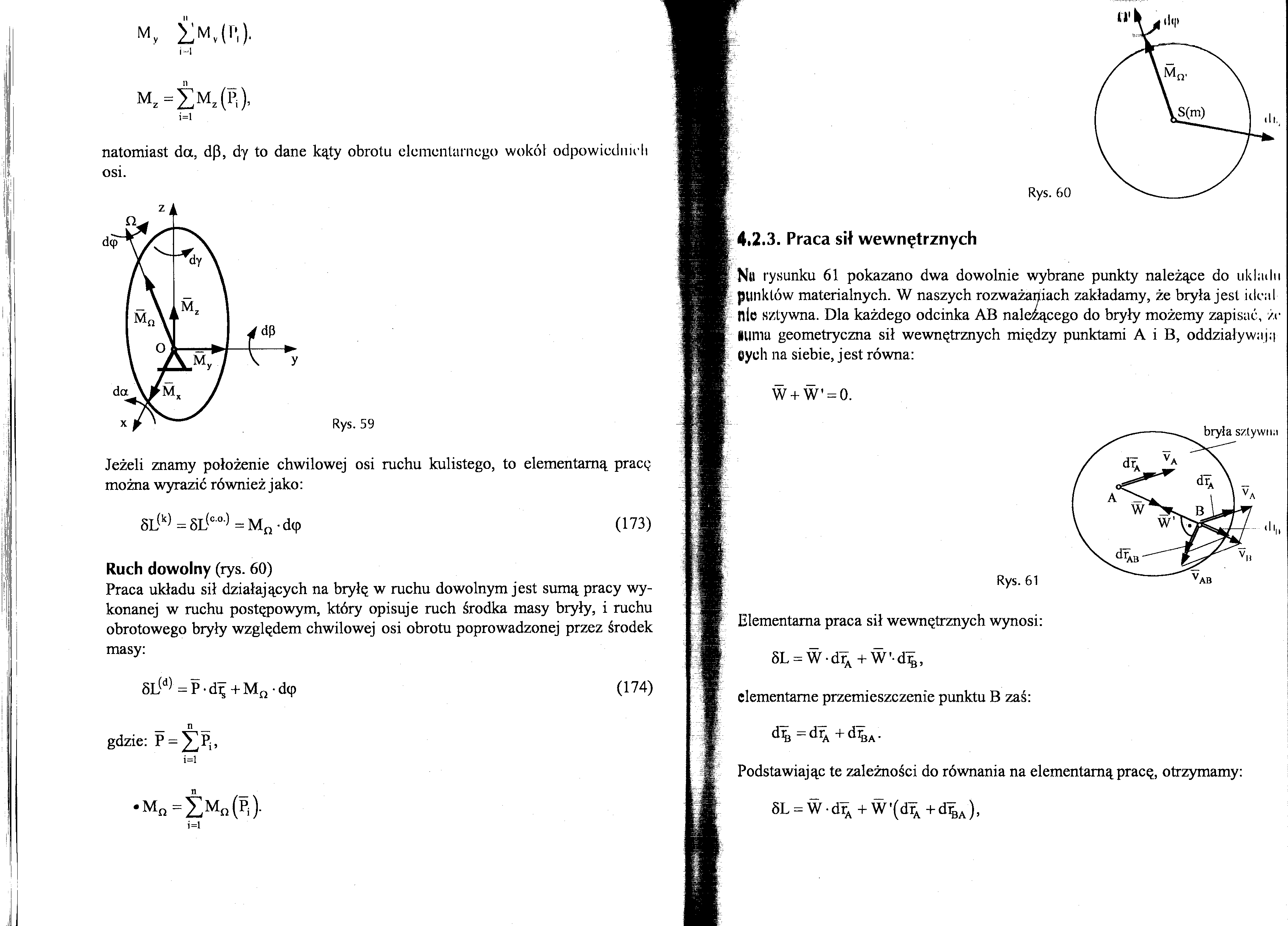
m, ix(p,).

M

i=l

natomiast da, dp, dy to dane kąty obrotu elementarnego wokół odpowiednich osi.

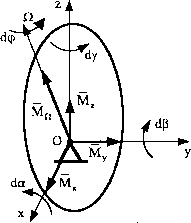
Jeżeli znamy położenie chwilowej osi ruchu kulistego, to elementarną pracę można wyrazić również jako:

8L^(k)=5L^(co)=M_n-dcp    (173)

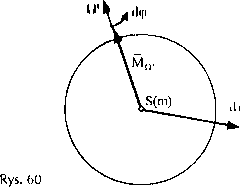
Ruch dowolny (rys. 60)

Praca układu sił działających na bryłę w ruchu dowolnym jest sumą pracy wykonanej w ruchu postępowym, który opisuje ruch środka masy bryły, i ruchu obrotowego bryły względem chwilowej osi obrotu poprowadzonej przez środek masy:

8li^d) = P•dę + M_n • dtp

gdzie: P = £Pj,

i=l

.M_n=Ś^Mo(Pi)-

i=l

4.2.3. Praca sił wewnętrznych

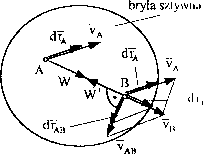
Nu rysunku 61 pokazano dwa dowolnie wybrane punkty należące do układu punktów materialnych. W naszych rozważaniach zakładamy, że bryła jest ideał nic sztywna. Dla każdego odcinka AB należącego do bryły możemy zapisać, że UUnia geometryczna sił wewnętrznych między punktami A i B, oddziaływa j;| eyeh na siebie, jest równa:

W + W' = 0.

Rys. 61

Elementarna praca sił wewnętrznych wynosi:

8L = W-d^+W'-d%, elementarne przemieszczenie punktu B zaś: d% =d?_A +dr_BA.

Podstawiając te zależności do równania na elementarną pracę, otrzymamy: 5L = W-dr_A+W'(dr_A+dr_0A),