Mechanika ogolna0009

IX

^m-^aMr=Z^Pir

ⁱ⁼¹    (38)

n

^m>aM<p=2X

i=l

Ponieważ a_Mr = r_M — r_m -tp² jest to wartość przyspieszenia radialnego, natomiast a_M(p = r_M • (p + 2r_m ■ <p to wartości przyspieszenia transwersalnego, wówczas dynamiczne równania ruchu masy w układzie współrzędnych biegunowych będą równe:

^m(r_M-rnT<i>²) = 2X

(39)

i=l

n

m(r_M ■ (p + 2f_m ■ cp) = ^P_ip

Jeżeli opisujemy ruch masy w naturalnym układzie odniesienia, to rzutując równanie (8) na oś styczną x i normalną n, dostaniemy:

^m‘^aMT=2X

(40)

1=4

n

^m-^aMn=Z^Pin

Jeśli wartość przyspieszenia stycznego a_Mt = r_M ■ ćp i przyspieszenia normalnego v² .

^aMn j^est znana, wówczas dynamiczne równania ruchu masy w układzie Pm

współrzędnych naturalnych t i n wynoszą:

m(^rM-9) = £^Pk

i=l

n

m

,Pm j

=ip„

Przykład 4

Punkt o masie m przemieszcza się po torze kołowym. Określić, ile wynosi siła imcisku podłoża w położeniu pokazanym na rys. 8, jeżeli wiadomo, że znamy |cj’,o prędkość V i promień krzywizny toru R.

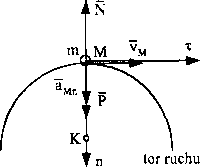
Rys. 8

Dane:

P - siła ciężkości [N],

R = K M - promień krzywizny toru [m], v - prędkość masy [m/s], przyspieszenie normalne masy:

a

Mn _{R R}

I )ymimiczne równanie ruchu na kierunku osi normalnej n będzie mieć postać:

m-^aMn =Z^Pin ^=P“^N>

■il:|il mamy:

N = P - m ■ a_Mn = ^p ■

P v^_

gR

p

Vr-v²>

s g^R >

/ tego wynika, że jeżeli g-R - V² = 0, czyli gdy prędkość masy v > yJg-R , wów-i zas w pokazanym na rys. 8 położeniu masa oderwie się od powierzchni, bo wówczas N < 0. Aby do oderwania nie doszło, prędkość masy w tym punkcie powinna być następująca:

V<yjg-R .

Przykład 5

Masa zawieszona na nierozciągliwej linie przemieszcza się w płaszczyźnie xy (i ys. 9). Opisać ruch masy.

Kuch masy odbywa się w płaszczyźnie xy. Ruch ten możemy opisać, przyjmując np. układ współrzędnych biegunowych r i (p. Dynamiczne równania ruchu masy hędi| wygli|diić naslępupii o:

^m(^VM 'mV) I]'

’_M — P ■ cos ip N

(42)