Mechanika ogolna0090

1 , 1 ,

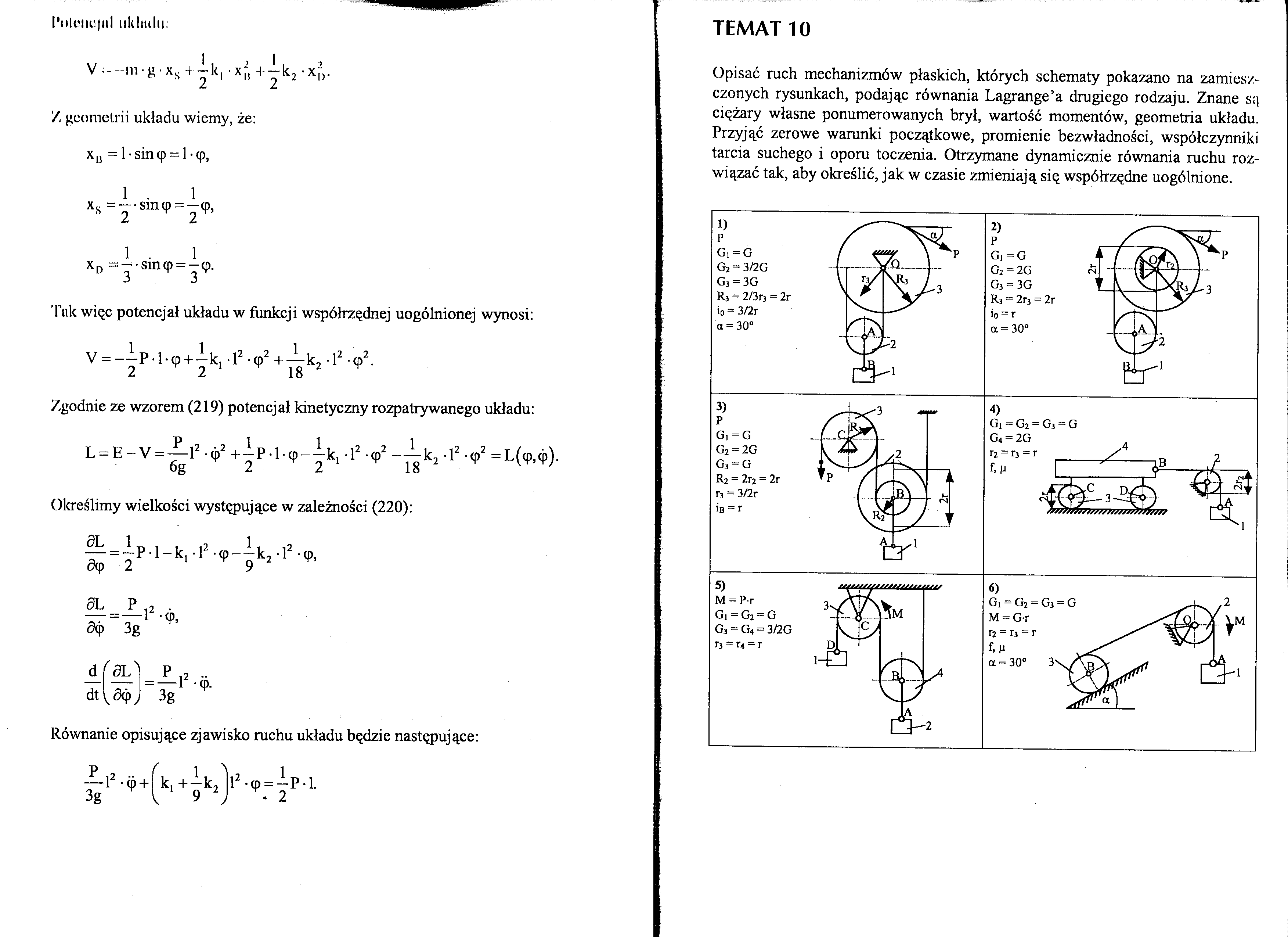
-ni'g'X_s +-k, ■ x„ 4k₂ -xj;

Z geometrii układu wiemy, że: x_u = 1 • sin tp = 1 - cp,

1 . 1 x^ = — • sm cp =—cp, ^s 2 2

1 . 1

x_n- — •sm(p =—cp. o _3    3^V

Tak więc potencjał układu w funkcji współrzędnej uogólnionej wynosi:

V = -—P-l-cp +—k, -l² -cp² +—k₂ -l² -cp².

2    2 ¹ 18 ²

Zgodnie ze wzorem (219) potencjał kinetyczny rozpatrywanego układu:

L = E - V =—l² • (p² + -P • 1 • cp --k, • l² • (p² -—k₂ • l² • (p² = L(cp, tp).

6g    2    2    ¹    18    ^2    v '

Określimy wielkości występujące w zależności (220):

—    = -P-l-k_rl²-cp--k₂-l²-<p,

Sep 2    ^{1 V} 9 ²

dL P ₂ .

—    =—1 -cp,

Sep 3g

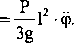
dYsiA

dt^Scp,

Równanie opisujące zjawisko ruchu układu będzie następujące:

—I² -tp + fk, + Av ]l²-cp = i-P-l.

3g l ¹ 9 ²J A2

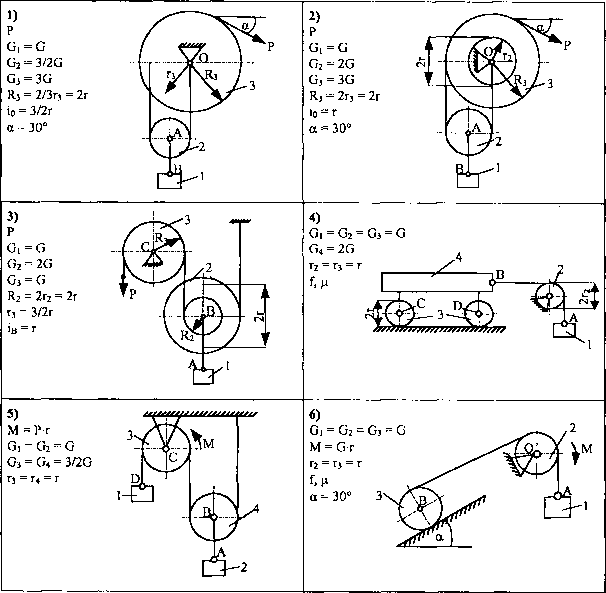
TEMAT 10

Opisać ruch mechanizmów płaskich, których schematy pokazano na zamieszczonych rysunkach, podając równania Lagrange’a drugiego rodzaju. Znane są ciężary własne ponumerowanych brył, wartość momentów, geometria układu. Przyjąć zerowe warunki początkowe, promienie bezwładności, współczynniki tarcia suchego i oporu toczenia. Otrzymane dynamicznie równania ruchu rozwiązać tak, aby określić, jak w czasie zmieniają się współrzędne uogólnione.