Mechanika ogolna0080

160

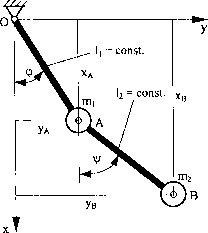
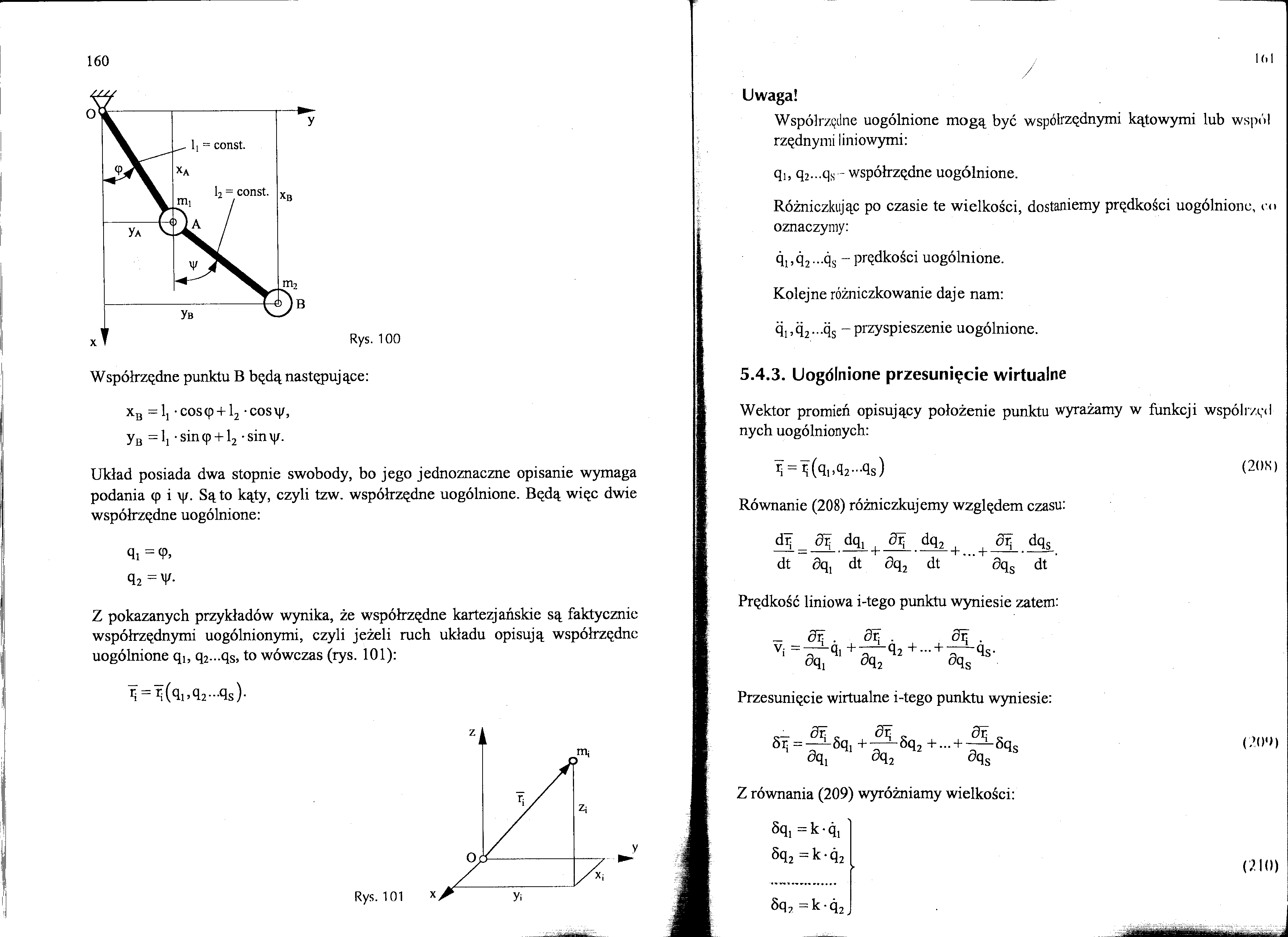
Współrzędne punktu B będą następujące:

x_B =lj -cos(p + l₂ COSV|/, y_B =1[ -sin(p + l₂ -siny.

Układ posiada dwa stopnie swobody, bo jego jednoznaczne opisanie wymaga podania cp i v|/. Są to kąty, czyli tzw. współrzędne uogólnione. Będą więc dwie współrzędne uogólnione:

qi=9.

q₂ =¥•

Z pokazanych przykładów wynika, że współrzędne kartezjańskie są faktycznie współrzędnymi uogólnionymi, czyli jeżeli ruch układu opisują współrzędne uogólnione q_b q₂...qs, to wówczas (rys. 101):

^ = ^(qi»q₂-qs)-

Rys. 101

1 (l 1

Uwaga!

Współrzędne uogólnione mogą być współrzędnymi kątowymi lub współ rzędnymi liniowymi:

qi, q₂...q_s- współrzędne uogólnione.

Różniczkując po czasie te wielkości, dostaniemy prędkości uogólnione, en oznaczymy:

q!,q₂ ...q_s - prędkości uogólnione.

Kolejne różniczkowanie daje nam: q_I,q₂...q_s - przyspieszenie uogólnione.

5.4.3. Uogólnione przesunięcie wirtualne

Wektor promień opisujący położenie punktu wyrażamy w funkcji współrzęd nych uogólnionych:

(20S)

^fai.Ms)

Równanie (208) różniczkujemy względem czasu:

_{=    +}    ^dqs

dt dq, dt Sq₂ dt 9q_s dt

Prędkość liniowa i-tego punktu wyniesie zatem:

_ dĘ . dq . dĘ . ^vi    +^-q₂ +-+T-^Lq_s-

&łi Sq₂    9q_s

Przesunięcie wirtualne i-tego punktu wyniesie:

dr _    9r    9r „

^Sri =—H +——8q₂ + ... + -—8q_s oqi    ^2    ^q_s

Z równania (209) wyróżniamy wielkości:

8q, = k-q,

Sq₂ -k^-q₂

8q₂ = k • q₂

(210)