Mechanika ogolna0070

140

Przykład 21

Określić reakcje układu płaskiego w punkcie C.

W punkcie C układu występują więzy typu podpora stała, której reakcję w płaszczyźnie xy przewidujemy jako dwie składowe wzajemnie do siebie prostopadłe. Przyjmujemy układ współrzędnych xy. Określamy składową Y_c. Podporę zastępujemy takim więzem, aby możliwe było przemieszczenie na kierunku Y_c (rys. 84).

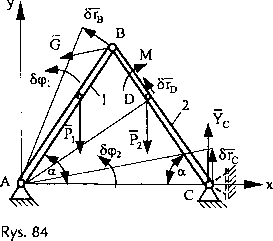
p¹1 - ciężary własne brył [N], a - kąt pochylenia bryły 1.

Dane:

AB = BC = 1 - wielkości geometryczne [m],

M - moment pary sił działających na bryłę 2 [N-m], G - siła czynna działająca na przegub B [N],

Określimy przemieszczenia przygotowane poszczególnych brył. Bryła 1 może obracać się dokoła punktu A. Bryła 2 jest w ruchu płaskim i jej środek chwilowego obrotu jest w punkcie A. Z kinematyki, z rozkładu prędkości możemy więc wykorzystać zależności na promienie i obroty przygotowane:

8r_B = AB • Sep! = AB • 8<p₂, bo v_B = ABco^ABgc^,

8r_c=AC-8(p₂,    bov_c=AC-G)₂.

Z geometrii układu wiadomo, że:

8r_c — 2 -1 -8cp₂ cosa,

8r_B = 1 • 8cp, = 1 • 8cp₂, czyli:

Sep, =8cp₂.

Praca przygotowana układu sił będzie równa: 8l, = 8L, + 8L₂ =0,

- I* • 1 • cos a + G • 1 • sin a 18<p,,

8L, =M_A -8cp|

8L₂ = P • 8^ + M_d ■ 8(p₂ = M_a • 8<p₂

2-Y_c -1-cosa-—P₂ -1-cosa-M J8(p₂,

SL = | P, -1-cosa + G -1-sina-f 2-Y_r -1-cosa-—P, -1-cosa-M ]——-.

2 ¹    2    J 2-1-cosa

ale:

8r_c ^ 0, czyli:

—^-(P, +3-P₂)l-cosa + G-l-sina + 2-Y_c -l-cosa-M = 0, stąd mamy:

_v    2 • M + (P, + 3 • P₂) 1 • cos a - 2 • G • 1 • sin a

— .

4- 1-cosa

Podobnie postąpimy, określając składową X_c w punkcie C.

Bryła 1 może wykonywać ru^lp obrotowy dokoła punktu A, bryła 2 jest w ruchu płaskim o chwilowym środku obrotu w punkcie C₂ (rys. 85):

8r₀ = AB-Scp, =BC₂ -8<p₂, bo v_B = AB -co, =BC₂ -oo₂, 8r_c = CC₂ • 8(p₂,    bo v_c =CC₂-ft)₂.

Bok AC₂ trójkąta ACC₂ wynosi:

AC

AC₂ = —— = 2 • AB = 2-1, cos a

CC₂=AC₂-AB = 1,

8r_B = 1 - 8<p, =l-8(p₂,

Sep, =8<p₂.