Obraz0033 2

66

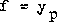
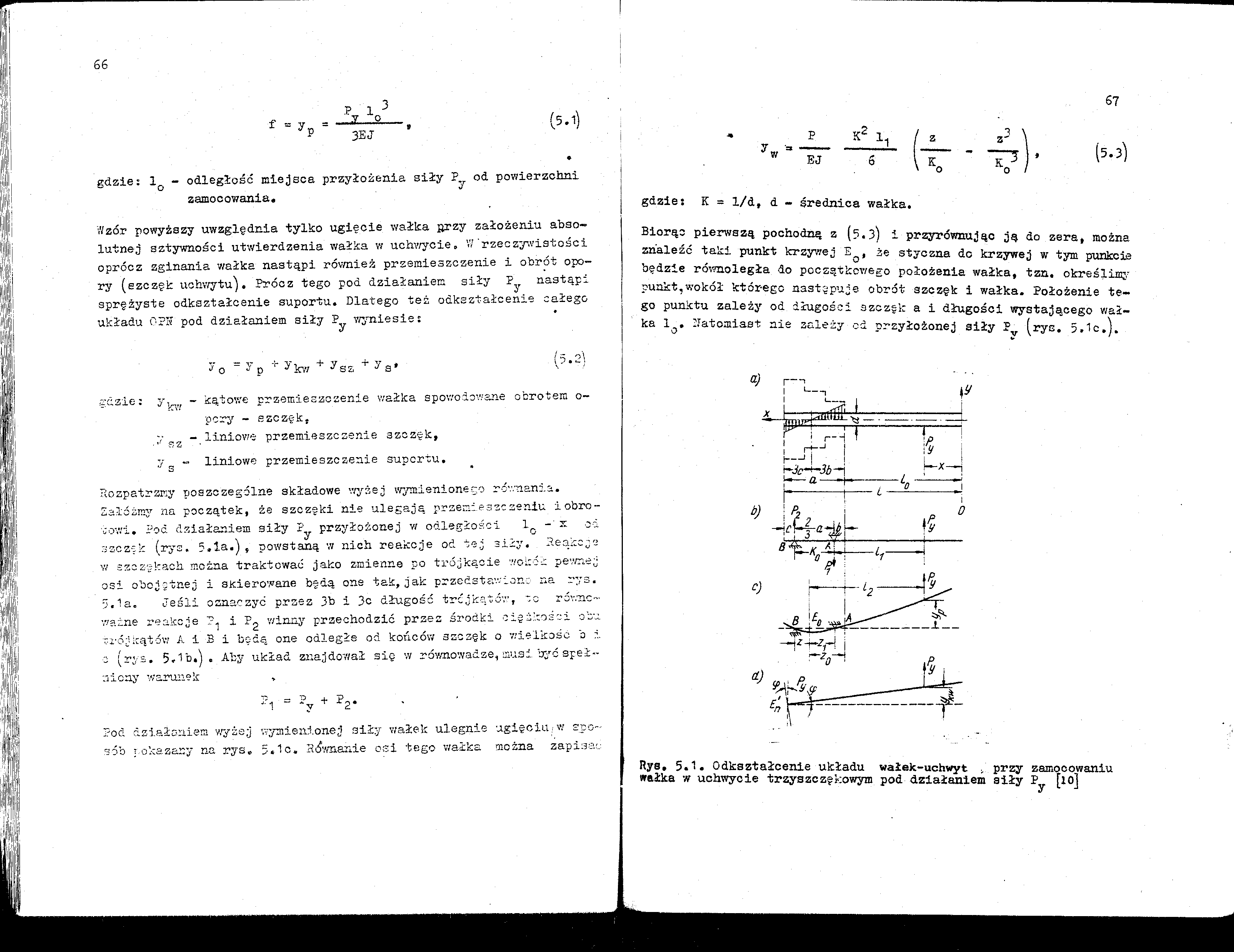
3EJ

9

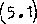
gdzie: 1_Q - odległość miejsca przyłożenia siły P od powierzchni zamocowania.

•Hzót powyższy uwzględnia tylko ugięcie wałka przy założeniu absolutnej sztywności utwierdzenia wałka w uchwycie, '//'rzeczywistości oprócz zginania wałka nastąpi również przemieszczenie i obrót opo-

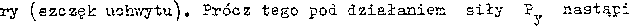
sprężyste odkształcenie suportu. Dlatego też odkształcenie całego

układu OPIf pod działaniem siły P^ Y/yniesie:

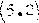
o “D ^r^kw ⁺ ^sz~^r*^,’s'

gdzie: y-_CT, - kątowe przemieszczenie wałka spowodowane obrotem o-pcry - szczęk,

y - liniowe przemieszczenie 3zczęk, y_o - liniowe przemieszczenie suportu.

Rozpatrzmy poszczególne składowe wyżej wymienionego równania. Załóżmy na początek, że szczęki nie ulegają przemieszczeniu i obrotowi. Rod działaniem siły ? przyłożonej w odległości 1₀ r od szczęk (rys, 5.la.), powstaną w nich reakcje od tej siły. Reąkepe w szczekach można traktować jako zmienne po trójkącie wodór pewnej osi obojętnej i skierowane będą one tak, jak przedstawione na rys. ę.la. Jeśli oznaczyć przez 3b i 3c długość trójkątów, cc równoważne reakcje ?, i Pg winny przechodzić przez środki ciężkości obu trójkątów A i B i będą one odległe od końców szczęk o wielkość b i •s (rys. 5,1b«) . Aby układ znajdował się w równowadze, musi być spełniony warunek    ,

^P1 = ^?y ^{+ ?}2*

Pod działaniem wyżej wymienionej siły wałek ulegnie ugięciu;w sposób r.okazany na rys. 5.1c. Równanie osi tego wałka można zapisać

gdzie: K = 1/d, d - średnica wałka.

Biorąc pierwszą pochodną z (5.3) i przyrównując ją do zera, można znaleźć taki punkt krzywej E_q1 że styczna do krzywej w tym punkcie będzie równoległa do początkowego położenia wałka, tzn. określimy punkt,wokół którego następuje obrót szczęk i wałka. Położenie tego punktu zależy od długości szczęk a i długości wystającego wał-

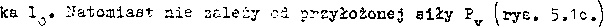
EJ

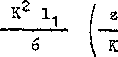
"o

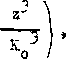
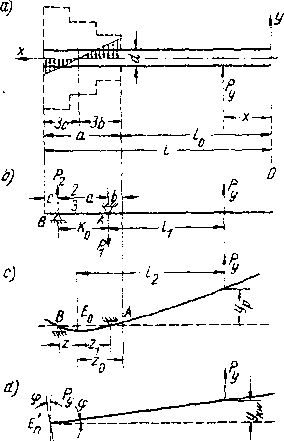
Rvs. 5.1. Odkształcenie układu wałek.-uchwvt . t>rzv zamocowaniu