P4180005

Przykład 2.9. Zbadać numeryczną poprawność następującego algorytmu rozwią-zywania równania kwadratowego z przykładu 2.6:

—»

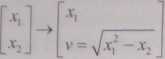
>1 = *, +^V1

y₂=x,-vj

Źródłem numerycznej niepoprawności może być w tym przypadku odejmowanie liczb bliskich sobie, które ma miejsce, gdy x₂ —> 0; wówczas bowiem błąd wyznaczania pierwiastka y₂ może rosnąć nieograniczenie, jako że nieogranicze-nie rośnie współczynnik przenoszenia błędu wyniku pierwiastkowania:

^K,.r =

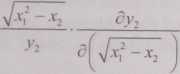
x₂ —*0

->oo

Klasyczny algorytm rozwiązywania równania kwadratowego nie jest więc numerycznie poprawny. Alternatywą jest algorytm wyznaczania y₂ wynikający z zastosowania wzoru Viete’a na iloczyn pierwiastków:

iv	U 1
	-> f-2—
UJ	[y, =^x,^+^^x, -x2

§

Nietrudno się przekonać, że eliminacja odejmowania doprowadziła do powstania algorytmu numerycznie poprawnego.

4

b

ja

Zadanie 2.7. Skonstruować numerycznie poprawny algorytm obliczenia wartości wyrażenia:

‘"■W*¹

Oszacować błąd obliczania y według tego algorytmu.

sz

2.4. ANALIZA DOKŁADNOŚCI ALGORYTMÓW ZA POMOCĄ KOMPUTERA

Podstawą analizy zadań i algorytmów numerycznych j [ /ynniknw nr/fnos/enia hk-Hów w Innkcii danvi't> ' ^Ł"”'

h\

Piej