Sieci CP str118

118

także wektory własne macierzy kowariancji C_xx. Istotnie, spróbujmy szukać punktu stałego W" w postaci W⁴ = pC*, gdzie C,- jest wektorem własnym macierzy C_xx odpowiadającym wartości własnej A<:

CxxC_{i =} Aj Cj

wówczas równanie 49L — 0 prowadzi do zależności

P o A, Ci - p² 0 (X^T C. ) C, = 0

której rozwiązanie ma formę

i ostatecznie

a A,-

^p ~ P(X? C,)

^w' - WWW) ^Ci

Podane wyżej rozwiązania (dla i = 1,2,... ,n) mogą być stabilne lub niestabilne. Można się o tym przekonać rozważając zmienność kąta 0 pomiędzy wektorem W“ i C,.

= E

{

'(*(iwpiM-

d (cr w)/,fi (<^wh(||w||)ąk

IK.ll m\²

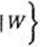
Po uwzględnieniu zależności Cj C_xx = A*Cf i po przekształceniach otrzymujemy za

leżność:

E

M (

l* VIKV||||W|!

) |wj =<r

cos 0

w^Tc_xxw\

iw ;

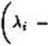
i dowolnego wektora V

Twierdzenie Rayleigha głosi, że dla dowolnej macierzy A_Xx spełniona jest nierówność

V^rA_xxV

||V||*    “ ^A""“

gdzie A_mnx jest największą wartością własną macierzy A. Stosując to twierdzenie do macierzy C_xx łatwo można stwierdzić, że rozwiązania opisujące przebieg procesu uczenia W(t) dążyć będzie do wartości W“ = pC_max. gdzie C_mnx jest. wektorem własnym odpowiadającym wartości własnej A_inax. Warunkiem jest jednak to, by w każdym momencie t zachodziła zależność W(t) > 0. Biorąc pod uwagę fakt, że wektor C_max jest oczywiście a’priori nieznany — trudno zagwarantować spełnienie tego warunku, przy czyni podstawowa trudność pojawia się przy ustalaniu punktu starowego dla procesu uczenia W(0), ponieważ oczywiście trzeba zapewnić spełnienie warunku W(0) > 0. Brak spełnienia wyżej sformułowanych warunków prowadzi zwykle od procesu uczenia, który jest. niestabilny (rozbieżny do nieskończoności) albo zbieżny do W* = 0.

Przypadek 5. Zagadnienie uczenia jest z założenia nieliniowe, gdyż tylko jedna funkcja jest liniowo zależna od y .<}> = ery, natomiast druga ma od początku formę nieliniową: -jr = fiy*. Wówczas

dW

— = _nyX-fly ^aW