skanuj0004

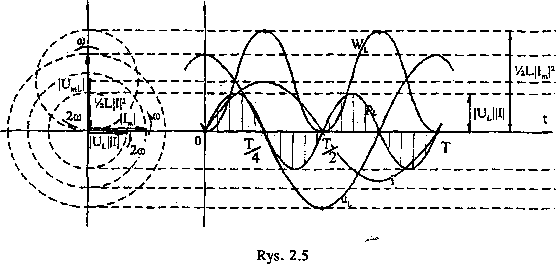
^4^L|/J2=i^{wi|/J2,    (2}-³⁹⁾

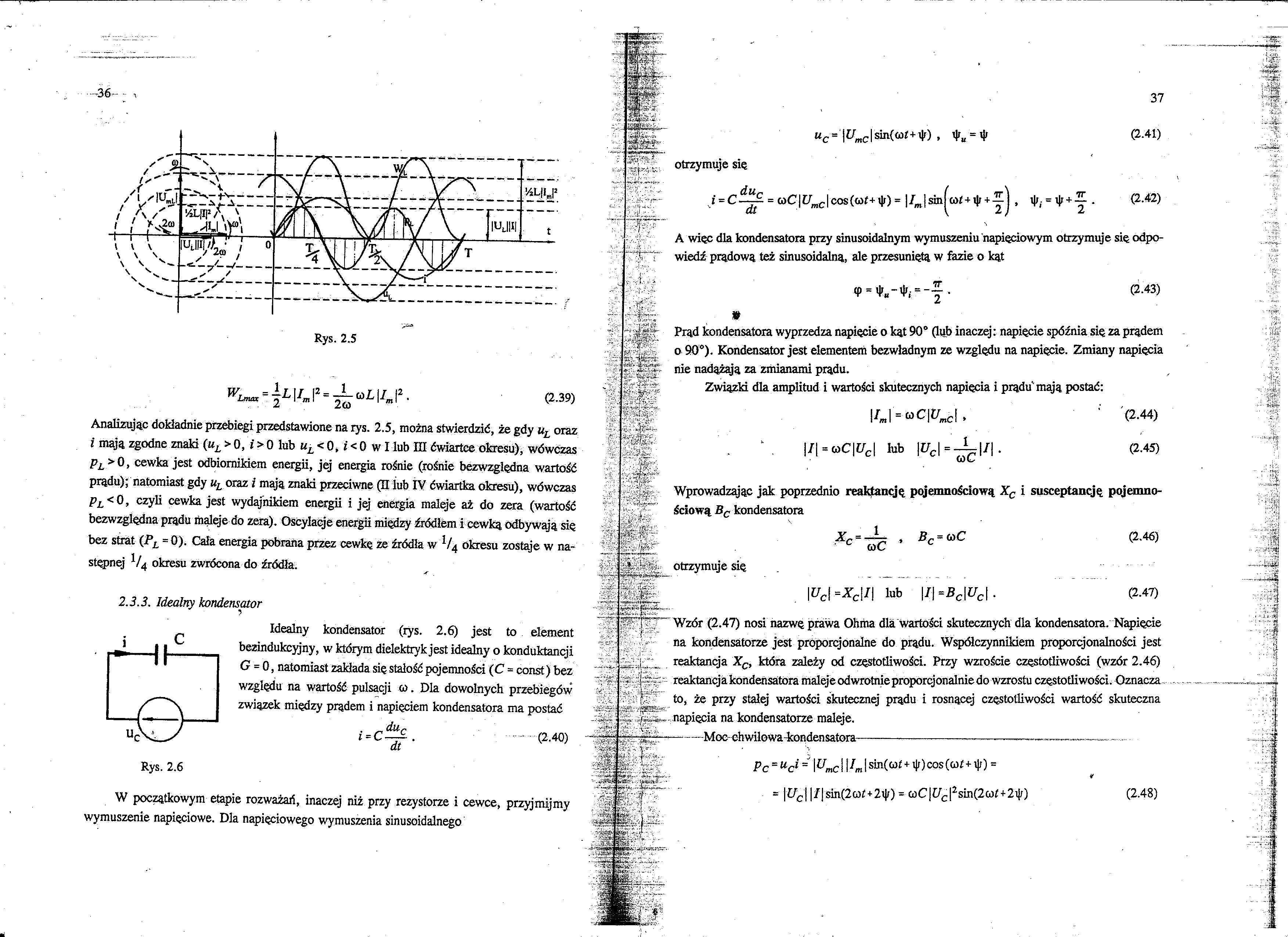
Analizując dokładnie przebiegi przedstawione na rys. 2.5, można stwierdzić, że gdy u_L oraz i mają, zgodne znaki (u_L > 0, i > 0 lub u_L < 0, i < 0 w I lub III ćwiartce okresu), wówczas p_L>0, cewka jest odbiornikiem energii, jej energia rośnie (rośnie bezwzględna wartość prądu); natomiast gdy u_L oraz i mają znaki przeciwne (II lub IV ćwiartka okresu), wówczas p_L<0, czyli cewka jest wydajnikiem energii i jej energia maleje aż do zera (wartość bezwzględna prądu maleje do zera). Oscylacje energii między źródłem i cewką odbywają się bez strat {P_L = 0). Cala energia pobrana przez cewkę ze źródła w ^!/₄ okresu zostaje w następnej V₄ okresu zwrócona do źródła.

2.3.3. Idealny kondensator

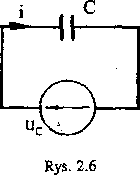
Idealny kondensator (iys. 2.6) jest to element bezindukeyjny, w którym dielektryk jest idealny o konduktancji G= 0, natomiast zakłada się stałość pojemności (C = const) bez względu na wartość pulsacji co. Dla dowolnych przebiegów związek między prądem i napięciem kondensatora ma postać

i-C^.    ...........(2.40)

dt

W początkowym etapie rozważań, inaczej niż przy rezystorze i cewce, przyjmijmy wymuszenie napięciowe. Dla napięciowego wymuszenia sinusoidalnego

u_c= |ł7_mC|sin(<ot+₁|r) , i|r,, = i|r    (2.41)

otrzymuje się

J=C^ = wC|i7_mC|c^os(wf+ilr)= |/_m|sin^+i|i + ^) , t, = i|r + y. (²-⁴²)

A więc dla kondensatora przy sinusoidalnym wymuszeniu napięciowym otrzymuje się odpowiedź prądową też sinusoidalną, ale przesunięta w fazie o kąt

₍p = ^_B-₁];. = -Z.    (2.43)

»

Prąd kondensatora wyprzedza napięcie o kąt 90° (lub inaczej: napięcie spóźnia się za prądem o 90°). Kondensator jest elementem bezwładnym ze względu na napięcie. Zmiany napięcia nie nadążają za zmianami prądu.

Związki dla amplitud i wartości skutecznych napięcia i prądu'mają postać:

^;    (2.44)

.    \    |/| = (oC\U_c\ lub |tf_c|=-^|/|.    (2.45)

Wprowadzając jak poprzednio reaktancją pojemnościową X_c i susceptancję pojemnościową B_c kondensatora

X_c = -^; , B_c = aC    (2.46)

0)C

otrzymuje się

\U_C\~X_C\I\ lub \I\‘B_C\U_C\.    (2.47)

““ Wzór (2.47) nosi nazwę prawa Ohma dla wartości skutecznych dla kondensatora. Napięcie na kondensatorze jest proporcjonalne do prądu. Współczynnikiem proporcjonalności jest reaktancja X_c, która zależy od częstotliwości. Przy wzroście częstotliwości (wzór 2.46) ■- reaktancja kondensatora maleje odwrotnie proporcjonalnie do wzrostu częstotliwości. Oznacza to, że przy stałej wartości skutecznej prądu i rosnącej częstotliwości wartość skuteczna „. napięcia na kondensatorze maleje.

——------Moc chwilowa kondensatora-——-— .............

Pc = k_c* = \^UmC I\L I ^sin(<^ ⁺ t|t)cos(<af'+ f) =

(2.48)

= |£7_C| |/|sin(2ut+2i|f) = cdC|K_c|²sin(2ut+2i|/)