skanuj0018

Ogólnie przedstawia się to tak:

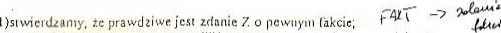
2)    ruńmy jakąś wiedzę W, tzn. ustaliliśmy, te pewne zdania si\ prawdziwe;    £

3)    chcemy znaleźć zdanie, które stanowiłoby rację dla zdania Z;    p

4)    z samych zdań tworzących naszą wiedzę W zdanie Z nie wynika;

5)    ąle ze zdania H (hipoteza) i zdań W łącznic zdanie Z wynika.

Istotną sprawą jest umiejętność określenia, w jakim stopniu dana hipoteza jest prawdopodobna, umiejętność sprawdzania hipotez i ewentualnie rozstrzyganie, jaką w danym przypadku przyjąć należy hipotezę spośród hipotez konkurencyjnych, to znaczy niezgodnych między sobą hipotez, które mogłyby służyć jako odmienne wyjaśnienia tych samych stwierdzonych przez nas faktów.

wigeej znajdziemy jej prawdziwych_następstw i tni oaiuziei_nasjępnwa ic są 'roźno£odne Przy czym przez sprawdzanie / wynikiem pozytywnym tym bardziej rośnie prawdopodobieństwo liipotezy, im mniej prawdopodobne wydawały się poprzednio owe znalezione kolejne następstwa hipotezy.

Gdyby nie udało się znaleźć takich znanych nam faktów, które pozwoliłyby obalić jedną z "konkurencyinych hipotez, trzeba zorgŁiuźóWić Odpowiedni eksperym^tpTa^r^pSźwohlOy potwierdzić iedna z nich, a jednocześnie obalić

pozostałe (txperitnentum crucis-)

Jeśli p^wtie fakty moźiut na gruncie naszej wiedzy wyjaśnić za pomocą jakiejś jednej tylko hipotezy (czy uzupełniającego się zespołu kilku hipotez), a wszelkie inne, konkurencyjne, hipolezy zostały przez nas obalone, to jesi rzeczą rozsądną uznać tę hipotezę za prawdziwą • tak, jak uznaje się wniosek we wnioskowaniu redukcyjnym.

Przyjmowanym hipotezom wyjaśniającym-stawia_s:ę miedzy innymLwymók. *hy.nie-Byly.Ło hipojczyjwmtilownne mi lioc.jo.wnczyją IkjcJcJjfoeJii.ejindnjajslę do wyjaśnienia jakichś Jmiydi-faktói^ioiii tym, którego wyjnśnicnla właśnie 52ukarnv.“hJTć'zatfawnh nas iri \wiaim**ri/*^Hial^r7TóT)'TaH/*s"nriTrczccÓIne S\ jest P,