skanuj0041

wskazówkami zawartymi w cz.I p.4.2 - 4.4.

4. Obliczyć wartość modułu sztywności G badanego drutu oraz maksymalną niepewność względną tego pomiaru (Ar, ATq, AT\ oznaczają niepewności maksymalne odpowiednich pomiarów):

Al	4-	4Ar		Ah	_L	2 A T0	+	2 Ar,
l	i	r		h	T	0 1		e-7 ? 0 1

5. Przeprowadzić dyskusję otrzymanych wyników.

5. Uzupełnienie

Rozważmy cylindryczny pręt o długości 1 i promieniu r, którego jeden koniec jest zamocowany nieruchomo, a do drugiego przyłożony jest moment skręcający M (rys.3). Moment ten powoduje skręcenie dolnego końca pręta względem górnego o kąt cp i każdy element drutu ulega deformacji prostego ścinania. Aby wyprowadzić związek pomiędzy modułem sztywności G a wartością momentu M sił skręcających drut, należy przyjąć, że pręt składa się z wielu cylindrycznych współosiowych warstw, które obracają się dookoła osi pręta. Prostopadłościenny fragment warstwy o promieniu x, grubości dx i długości ds zostaje odkształcony, jak pokazano na rys.3, a pomiędzy kątem skręcenia 9 i kątem ścinania a zachodzi związek:

<px = al.

Zgodnie z prawem Hooke’a naprężenie styczne dane jest wzorem:

r=Ga=GSŁ,    (10)

Naprężenie ścinania r jest równe sile stycznej dF działającej na brzeg równo-ległoboku, do pola powierzchni przekroju:

=

cbcds ’

Wartość momentu siły względem osi pręta wynosi:

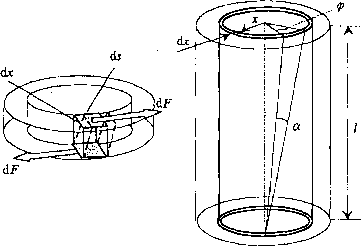
Rys.3. Schematyczne przedstawienie warstw cylindrycznego, skręcanego pręta

dM = xdF = Trcbcds.

Wartość momentu skręcającego dla cylindrycznej warstwy o grubości dr jest sumą takich momentów sił po pełnym obwodzie koła s = 2tcc:

dM =TrdrJds = 27tTx²dx.

Całkowity moment sił działający na pręt otrzymamy sumując przyczynki do momentu od wszystkich współosiowych rurek, od x = 0 do x = r. Uwzględniając wzór (10) otrzymujemy:

M ~ \dM = 27iG— jV dx = ⁷¹ Gr ę .    (11)

o    l o    2/

Literatura

[1]    H.Szydłowski: Pracownia fizyczna, PWN, Warszawal994.

[2]    R.P.Feynman, R.B.Leighton, M.Sands: Feynmana wykłady z fizyki, t.II, cz.2, PWN, Warszawa 1970.

[3]    J.Massalski, M.Massalska: Fizyka dla inżynierów, t.l, WN-T, Warszawa 1975.