skanuj0041

80

wskazówkami zawartymi w cz.I p.4.2 - 4.4.

4. Obliczyć wartość modułu sztywności G badanego drutu oraz maksymalną niepewność względną tego pomiaru (Ar, A7o, AT) oznaczają niepewności maksymalne odpowiednich pomiarów):

A /	+	4A r		A/,	X	2 A T0	i	2 A 7j
/		r	T ,	h	T	l-(Tl/To)^2 T0	T*	l-fo/r,)^1 t,

5. Przeprowadzić dyskusję otrzymanych wyników.

5. Uzupełnienie

Rozważmy cylindryczny pręt o długości 1 i promieniu r, którego jeden koniec jest zamocowany nieruchomo, a do drugiego przyłożony jest moment skręcający ii/(rys.3). Moment ten powoduje skręcenie dolnego końca pręta względem górnego o kąt cp i każdy element drutu ulega deformacji prostego ścinania. Aby wyprowadzić związek pomiędzy modułem sztywności G a war-’ (ością momentu M sił skręcających drut, należy przyjąć, że pręt składa się z wielu cylindrycznych współosiowych warstw, które obracają się dookoła osi pręta. Prostopadłościenny fragment warstwy o promieniu x, grubości dx i długości ds zostaje odkształcony, jak pokazano na rys.3, a pomiędzy kątem skręcenia (p i kątem ścinania a zachodzi związek:

<px = al.

Zgodnie z prawem Hooke’a naprężenie styczne dane jest wzorem:

r= Ga= G^~-,    (10)

Naprężenie ścinania r jest równe sile stycznej dF działającej na brzeg równo-Icgłoboku, do pola powierzchni przekroju:

dF

cbcd s’

Wartość momentu siły względem osi pręta wynosi:

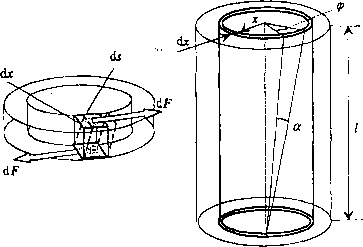
Rys.3. Schematyczne przedstawienie warstw cylindrycznego, skręcanego pręta

dM = xćF = Tjcdcds.

Wartość momentu skręcającego dla cylindrycznej warstwy o grubości dr jest sumą takich momentów sił po pełnym obwodzie koła s = 2rac:

dM =rxdx|ds =2JtTx²dbc.

Całkowity moment sił działający na pręt otrzymamy sumując przyczynki do momentu od wszystkich współosiowych rurek, od x - 0 do x = r. Uwzględnia-j ąc wzór (10) otrzymuj emy:

M = JdM = 27tG— jx³ dx - ^ ^r ę .    (11)

o    l o    21

Literatura

[1]    H.Szydłowski: Pracownia fizyczna, PWN, Warszawal994.

[2]    R.P.Feynman, R.B.Leighton, M.Sands: Feynmana wykłady z fizyki, t.II, cz.2, PWN, Warszawa 1970.

[3]    J.Massalski, M.Massalska: Fizyka dla inżynierów, t.l, WN-T, Warszawa 1975.