Scan0049

Rozdział 6

Funkcje jako relacje

6.1 Funkcja

Definicja 6.1 Dla danych dwóch zbiorów X i Y, funkcją (odwzorowaniem, przekształceniem) o argumentach x £ X i wartościach y EY nazywamy relację binarną, określoną podzbiorem R C X x Y, która spełnia warunek, ze dla każdego argumentu x istnieje dokładnie jedna wartość y o własności (x,y) £ R:

1- A V ^xRy’

xEX y£Y

* A A {{xRy\ A xRy₂) => yi = y₂] •

yi,y₂€Y

Dla oznaczenia funkcji używamy liter /, p, h i piszemy:

xfy lub (x, y) £ f lub y = / (x).

Uwaga 6.1 Symbol f oznacza samą funkcję (zbiór), zaś f (x) oznacza wartość funkcji dla argumentu x. Argument x nazywamy także zmienną niezależną, a wartość y — zmienną zależną.

Definicja 6.2 Dziedziną Df funkcji nazywamy zbiór argumentów:

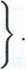
^Df = |^x: V y⁼ f (*)

l y