skanuj0150

298

zmianami energii, rejestrują tylko wartości średnie.

Ze wzoru (9) widać, że do obliczenia I konieczna nam jest znajomość E^lm. Rozważmy najprostszy przypadek, gdy nakładają się na siebie dwie fale elektromagnetyczne z identycznych źródeł (co_l = co₂), o amplitudach E\_m oraz E_2m, różniące się jedynie fazami początkowymi <f>\ i fc. Drgania wektora natężenia pola elektrycznego w elektromagnetycznej fali płaskiej zapiszmy tym razem w postaci funkcji zespolonej (sens fizyczny ma część rzeczywista, którą wydziela się w ostatecznym wyniku). Wektor E wypadkowej fali będzie równy:

E = E_lme*^k *) + E_lme^i{k^

gdzie: r\-r+S\ r₂=r są odległościami odpowiednio źródła 1 i źródła 2 od punktu P, k - Wektorem falowym. Obliczmy kwadrat amplitudy fali wypadkowej:

El=E-E* =

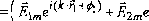
,Kk-h^+lh.)\-'a<

• ( E_lme~^i(k'^Fi⁺ A) + E_2me~^i(k^) j_e^ia)l,

skąd po przekształceniu otrzymujemy:

(10)

El =£>,,+E}_m+2E_lmE_2mcosA<p ,

gdzie: Atp -kó + {j\ -<t>f) jest różnicą faz. Podstawiając (10) do (9) dostaniemy, że:

/ = 7j +I₂ +2^IJ₂ cos Aę ,

(11)

gdzie l\ i h są natężeniami fal składowych. Iloczyn:

2-^1 _X12 cosAę»

(12)

występujący we wzorze (11) nosi nazwę wyrazu (członu) interferencyjnego, od jego bowiem wartości zależy, czy wystąpi zjawisko interferencji. Jeśli fale składowe są spójne, człon ten ma określoną, stałą w czasie wartość (lecz inną w różnych punktach przestrzeni), zależną od różnicy faz. Obserwujemy wówczas znane nam już maksima (dla Acp =2nn) i minima (dla Aę =(2n+l)rr). W

w

przypadku fal niespójnych, gdy różnica faz Aę zmienia się w czasie i przy długim czasie obserwacji, średnia wartość ^cos Aę ) = 0 i wartość wyrazu interferencyjnego (12) równa się zeru, natężenie fali wypadkowej wynosi:

/ = /_I+/₂,

i mamy do czynienia ze zwykłym sumowaniem się natężeń każdej z fal osobno, a interferencji nie obserwujemy.

Załóżmy, że t/\=tj>i i że różnicę faz Aę powoduje jedynie różnica dróg optycznych, tj. Aę =k-S, gdzie S=dsma (wzór (4) i rys.2). Wyraz interferencyjny (12) przyjmuje wówczas największą wartość dla Aę = 2nn, czyli dsina = nl, a minimalną dla Aę =(2n+l)n. Dostaliśmy więc analogiczny warunek na występowanie maksimów interferencyjnych jak (5).

W naturalnych źródłach światła poszczególne atomy emitują ciągi fal o skończonym czasie trwania (rzędu 10 ⁸ s) i długości (ok. 3m) w sposób zupełnie chaotyczny. Różnica faz Aę zmienia się więc również przypadkowo. Przy odpowiednio dobranych warunkach doświadczalnych możliwe jest uzyskanie obrazu interferencyjnego nawet używając takich źródeł. Przykładem jest doświadczenie Younga, gdzie interferują ze sobą wiązki światła wychodzące z dwóch szczelin oświetlonych przez jedno źródło. Jednak idealnymi źródłami światła do badania zjawisk interferencyjno-dyfrakcyjnych są lasery, dające światło spójne.

5.2. Dyfrakcja

Dyfrakcja jest to zjawisko polegające na uginaniu się fal padających na przeszkody lub przechodzących przez szczeliny. Szczelina zrobiona w nieprzeźroczystej przesłonie przepuszcza światło uginając je jednocześnie. Skończonych rozmiarów szczelinę możemy potraktować jako sumę bardzo wielu małych, stykających się ze sobą otworków, z których każdy jest, zgodnie z zasadą Huyghensa, źródłem elementarnej fali kulistej. Fale elementarne wychodzące z tych punktów interferują ze sobą i na ekranie powstają jasne i ciemne prążki dyfrakcyjne.

Dla kierunku na wprost wszystkie fale elementarne przebywają w przybliżeniu te same drogi optyczne i nakładają się na siebie z tymi samymi fazami (im większa jest odległość L szczeliny od ekranu w stosunku do szerokości samej szczeliny a, tym lepsze jest to przybliżenie). Mamy więc przypadek