Slajd47
&
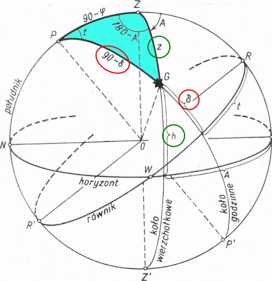
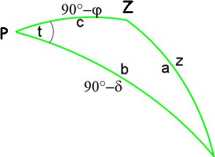
Azymut ciała o znanym kącie godzinnym t
sin a sin B = sin b sin A
sin a cos B = cos b sin c - sin b cos c cos A
znane są: t, 8, q>
sin(z)sin(180~A) = sin(90~S)sin(t) sin(z)cos(180-A) = cos(90-S)sin(90~cp)~ sin(90~S)cos(90-cp)cos(t)
sin(z)sin(A)=cos(s)sin(t)
sin(z)sin(A)=~sin(s)cos(cp)+cos(s)sin(cp)cos(t)
tg(A) =
sin(t)
sin(cp)cos(t)-tg(8)cos(q>)
np. 22. VI. t=6h 5=23°26‘ tp=53°26' (Szczecin) tg(A)=l ,0/(-0.4334*0.5958)= -3.873 A=104°29'
Wyszukiwarka
Podobne podstrony:
Slajd48 grlUIZpoBAzymut ciała o znanej odl. zenitalnej z znane są: z, 8, q>cos a = cos b cos c +
Slajd41 2 Trygonometria sferyczna Podstawowy zestaw wzorów: sin a sin B = sin b sin A cos a = cos b
Slajd4 (71) Ciała • Warstwy w trakcie powstawania są zazwyczaj ułożone poziomo skalne
Slajd45 Odległość zenitalna (wysokość) ciała z = 90° - h cos a = cos b cos c + sin b sin c cos A [a=
Slajd42 Moment siły działający na ramkę z prądemM = (IS)B sin <9 Dipolowy moment magnetyczny:
Slajd46 2 Długość dnia oraz momenty wschodów i zachodów z=90° o h=0° cos a = cos b cos c + sin b sin
462 (13) 462 PRZYKŁAD 15.3 RYS. 15.4 15. Ruch płaski ciała sztywnego zaś dla drugiegoP2 -XOr — Pi si
zad7 Zadanie 7 ClearAIlfGlobal *"] x = A*Sin[w*t + alfa] (* wychylenie ciała z położenia równo
Slajd41 Moment siły działający na ramkę z prądem Ma1 = ^ =
Slajd40 Trygonometria sferyczna Współrzędne prostokątne C w układzie XYZ: x = sin b sin A y = -
Slajd41 Moment siły działający na ramkę z prądem Ma1 = ^ =
Slajd42 Moment siły działający na ramkę z prądemM = (IS)B sin <9 Dipolowy moment magnetyczny:
Slajd42 c cos a = cos b cos c cos b = cos c cos a cos c = cos a cos b + sin b sin c cos A + sin
Slajd43 Trygonometria sferyczna trójkąt prostokątny cos a cos a sin b sin c = cos B cos C
Slajd46 2 Długość dnia oraz momenty wschodów i zachodów z=90° o h=0° cos a = cos b cos c + sin b sin
więcej podobnych podstron