462 (13)

462

PRZYKŁAD 15.3

RYS. 15.4

15. Ruch płaski ciała sztywnego

zaś dla drugiego

P₂

-XOr — Pi sin fi — S

8

Io2<h — Sr₂

Dopiszemy jeszcze równanie więzów. Gdyby nić nie mieszczała się względem klina, punkt A byłby chwilo^ środkiem obrotu dla pierwszego walca i wtedy ip, = _r • czyli xq\ = ri ip. Nić uzyska jednak pewne nieznane p^' spieszenie a. Załóżmy, że będzie ono skierowane jak ^ rys. 15.3. Zatem punkt A ma przyspieszenie równe co ^ wartości a, o zwrocie przeciwnym do zwrotu X\. W zwią^ z tym przyspieszenie środka 0\ będzie równe

x_0l = r\ip\ -a

a punktu 0₂

xo2 — ^r2<h + a

W wyniku rozwiązania układu tych sześciu równań o sześciu niewiadomych dostajemy

P₂ sin fi — Pi sin a ^a==g Pi + P₂

Pi ^2(sin ot + sin fi)

K| 3(Pi + P₂)

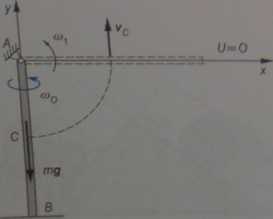
Jednorodny pręt AB o długości 2a i ciężarze P wisi pionowo na przegubie płaskim A. Jaką prędkość kątową too należy nadać temu prętowi, aby po oswobodzeniu go w chwili, gdy tworzy on z pionem kąt a = —, od więzów (przegubu A) pręt uderzył pionowo o podłogę (rys. 15.4)?

ROZWIĄZANIE

Obliczymy najpierw, jaką prędkość kątową a>\ ma pręt w chwili, gdy znajduje się w położeniu poziomym. Obliczymy % wychodząc z zasady zachowania energii mechanicznej

E₀ ■+■ Uo ⁼    + U\

Jeżeli przyjmiemy, że energia potencjalna pręta w położeniu poziomym jest równa zeru, otrzymamy

1,2 1 „ ,

-7_ag>₀ — mga = -1_A to\