461 (14)

15. Ruch płaski data sztywnego

461

Na środek walca działa siła F. Praca sił zewnętrznych zgodnie ze wzorem (15.2) jest równa

L = (F - T)x + Trę — (F- T)x + Tx = Fx Zatem praca sił tarcia T w tym przypadku jest równa zeru.

jednorodny walec o ciężarze P, długości 21 i promieniu r PRZYKŁAD 15.1 spoczywa na dwóch podporach (rys. 15.2). Znaleźć reakcje w punkcie A, w chwili gdy podpora B zostanie nagle usunięta.

ROZWIĄZANIE

RYS. 15.2

Równania różniczkowe ruchu walca przyjmą postać

ml

g

-xc — r — r h:H> — RąI

Dopiszemy jeszcze jedno równanie wynikające z równania więzów

lip = x_c

Moment bezwładności walca względem osi przechodzącej przez środek masy jest równy (przykład 12.1)

Po rozwiązaniu układu równań dostajemy

3r² +16/² Ra~^P 3r² + SP

PRZYKŁAD 15.2

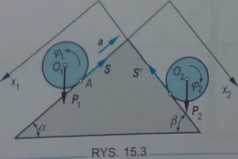
Dwa jednorodne walce o ciężarach Pi i P2 oraz promieniach n i ri owinięto nieważką nierozciągliwą nicią. Walce odwi-jające się z nici staczają się po równiach nachylonych w stosunku do płaszczyzny poziomej pod kątem a i /? (rys. 15.3). Znaleźć przyspieszenie a nici względem klina oraz napięcia nici S.

ROZWIĄZANIE

Przecinając myślowo nić, rozdzielamy układ na dwa układy proste. Równania ruchu pierwszego układu mają postać

H .. o . _c —xo_t — P\ sin ot — S 8

Iorfi = $n