472 (13)

472

15. Ruch płaski ciała sztywnego

ROZWIĄZANIE

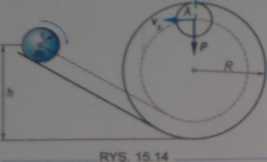
Wiadomo, że w czasie toczenia się bez poślizgu mimo wya powania sity tarcia można stosować zasadę zachowania energii mechanicznej

1.1, „

mgh m -av, + -ZfSr + mg(2R - r i

. .    _ W

gdzie a = —.

r

Gdy kulka znajduje się w punkcie 4, silą B_a potiaiM większa od sity ciężkości, co jest warunkiem przebycia cdJ pętli. Stąd w przypadku granicznym dostajemy

. ^v*

mg*«—

= g(R ~ r)

Po wstawieniu tej zależności do równania (1) uzyskamy

mgh *    — r) + - J,a? + mg(2R -r)    (2)

i stąd

h = 2R - r + i(R - r)( 1 +    )

2    \    mr²)

2    7

Dla J, = -mr, h = 2lt — r + ~(J? — r).

W szczególnym przypadku, gdy mamy do czynieni* z zsuwającym się punktem (r = 0, 7, = 0), z zależności

(2) otrzymujemy h = -R.

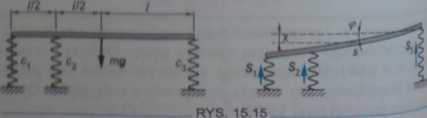
PRZYKŁAD 15.13 Ułożyć równania różniczkowe ruchu jednorodnej belki popartej na trzech sprężynach o współczynnikach utywsoto ct,C2,C3 (rys. 15.15). Odkształcenia sprężyn traktować jak¹ małe.