466 (10)

466

mig + 2P

01 = —

*1 =

15. Ruch płaski ciała sztywnego

. ^m\

w obu niciach. Dla jakiego stosunku mas — ciężarek«.

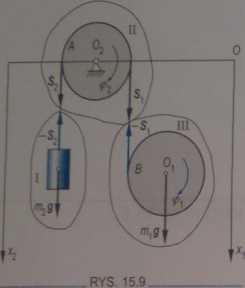
zostanie w spoczynku, jeżeli w chwili początkowej by) ^ 1 w spoczynku? Czy oś walca B może podnosić się do gu Jak zmieni się sytuacja, gdy w miejsce ciężarka na końcu ^ I przyłożymy siłę równą co do wartości P (rys. 15.9)?

ROZWIĄZANIE

Rozdzielimy układ na trzy układy proste. Układ I porusza* 1 ruchem postępowym, układ II ruchem obrotowym, zaś uklgj V ID ruchem płaskim. Równania różniczkowe ruchu tego układi | przyjmą postać

m2*2 = mig - S2

l<hjfo w ^si^r ~ ^S*^r m\X\ = mig — S\

fipf=

gdzie przez x\ oznaczono przyspieszenie środka Oj. | Dochodzą tu jeszcze dodatkowo dwa równania więzów j

x\ = r<j>\ # rę₂ iii = —ripi

Po rozwiązaniu układu równań (l)-r(6) otrzymamy

1 ..H ipm₂ - mi)    _ lm\mi

*2 = -Z--7-8’    ^s2 = 7—77—8

5mi + om₂.    5 mi + om2

mj(4m₂ -|- m\)    2ro₂

¹ 5mi + 6m₂    ¹ 5mi +6012^

Widzimy, że jeżeli mi = 3 m₂, ciężarek będzie znąjdotij się w spoczynku. Ponieważ Jq jest zawsze dodatnie, więc pm |

dowolnym stosunku mas —, oś Oj walca B zawsze tj mi

przemieszczać się w dół.

Gdy w miejsce ciężarka umieścimy siłę P, będzie® I mieli inny układ równań. Wówczas równanie (1) odpada,# ¹ nanie (2) zaś przyjmie postać

HfSf = Sir - Pr Rozwiązujemy układ równań (3)^(7) (równanie (6) j* teraz niepotrzebne) i otrzymujemy

4mig — 2 P

5    ’    5mi

Widzimy, że jeżeli P > 2m\g, to oś Oi walca B przemieszczać się do góry.