469 (6)

— cosąp.

15. Ruch płaski dała sztywnego

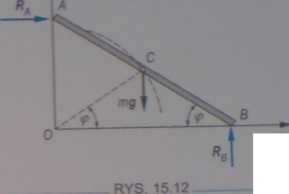
gtadkte. pręt zaczyna się zsuwać w dół bez prędkości począt-hwej. Wyznaczać prędkość kątową i przyspieszenie kątowe pięta oraz kąt pi, jaki pręt tworzy z poziomem w chwili, gdy przestanie się on stykać ze ścianą (rys. 15.12).

ROZWIĄZANIE

Energia kinetyczna pręta jest równa

E = i/(V + 2^mvc

ftaieważ współrzędne środka masy mają postać a    a .

yc = ~ suup

więc środek masy porusza się po okręgu o promieniu — i vc = a.

= -p, zatem

1 o . o 1 jj 1 o.o

E = —ma~<p~ + —maę = -ma ę 24    8    6

Energia potencjalna

U = mga — sin ę

Z zasady zachowania energii mechanicznej dostajemy równanie

*ł

1

1

1

-marę² + —mga sin ę = -mga sin ęo 6 2 2

stąd

ę = J^-isinęo — sinę>)

Zróżniczkowanie równania względem czasu daje nam 2

—ma²ęę + mgaę cos ę = O

stąd

3 g

ę —--cos ę

2a

Równania różniczkowe ruchu pręta mają postać mx_c = Ra myc = Rb — mg I_cę = E_B-cosę - R_A-sinę