121984

a _a = a_B = ac

dMO

dr 4. Ruch obrotowy dala sztywnego

Jeżeli unienichomimy dwa dowolne punkty bryły sztywnej, to wszystkie punkty leżące na prostej łączącej te dwa punkty (będące niemehome, stanowiące oś obrotu) będą mogły poruszać się po okręgach w płaszczyznach prostopadłych do osi obrotu o środkach na niej leżących.

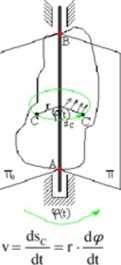
Tor każdego ciała poruszającego się ruchem obrotowym jest okręgiem leżącym w płaszczyźnie prostopadłej do osi obrotu o środku leżącym na tej osi i opisany jest promieniem o długości równej odległości punktu od osi obrotu. Sc=<p(t) r Prędkość liniowa

= «Kt)r = ®(t)r Prędkość kątowa o).

WIELKOŚCI KĄTOWE (określają ruch całej bryły)	WIELKOŚCI LINIOWE (dotyczą tylko określonego punktu )
<p = <p(t) - droga |rad)	^= (0 l^ml
dtp -= tu - prędkość [rad/s] dt	dsc -—- = Vc [m/s| dt
dtu -= € - przyspieszenie dt [rad/s^2l	dvr - , -= ac |m/s‘) dt

Sę=<P(t)T _ v_c =<yx r _c

— n —r

a_c

— n

a_c

Kierunek przyspieszenia normalnego równoległy do promienia CO. zwrot od C do O.

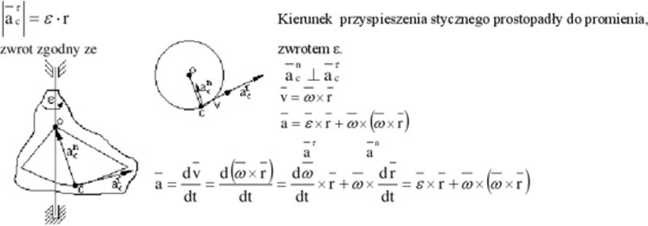
— a c + a c = co² -r

5. Ruch płaski dała sztywnego: równania ruchu: metody wyznaczania prędkości i przyśpieszeń

To nich w- którym wszystkie punkty ciała poruszają się w płaszczyznach równoległych do płaszczyzny zwanej płaszczyzną kienijącą.

Ruch płaski bryły sztywnej można przedstawić:

-jakopizemieszczenie i obrót

- jako obrót wokół szczególnego punktu

Ruch płaski jako złożenie przemieszczettia i obrotu

Równania:

Xb=Xb(0

yB=yB(t)

Xa=Xa(0

yA=yA(t)