465 (13)

465

15. Ruch płaski ciała sztywnego

po rozwiązaniu tego układu równań dostajemy

P\Q<Q + *P\)

¹    0(0 + 3Ą) +    + 30)

⁵² ~ 0(0 + 3F₂) |j /»|(8Ą + 30)

..    40(0 + 2/>i -h2P₂)

*³ “ 0(0 + 3Ą) + KSl + 30)*

PRZYKŁAD 15.6

c

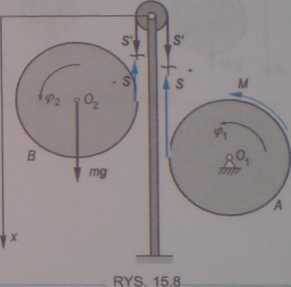
Dwa jednorodne krążki 4 i B o jednakowych promieniach r i masach m są owinięte nieważką nicią, przerzuconą przez mały blok C. Krążek A jest umocowany na stałej poziomej osi Q|. Na krążek ten działa stały moment M (rys. 15.8). Znaleźć przyspieszenie osi 02 krążka B oraz napięcie nici S. Znaleźć wartość momentu M, przy którym oś krążka B będzie się podnosić do góry. Masę bloku C zaniedbać.

ROZWIĄZANIE

Rozdzielimy układ na dwa układy proste. Pierwszy układ będzie się poruszał ruchem obrotowym, drugi ruchem płaskim. Równania różniczkowe ruchu tego układu przyjmą postać

Io\<P\ — M — Sr m'x₀₂ = mg — S Ithih = Sr

Przyspieszenie środka O2 jest równe

*02 = ^rih - ^riP\

momenty bezwładności zaś

i    1    ₂

l₀\ =102 = -mr

Po rozwiązaniu tego układu równań dostaniemy mgr + M    2(2mgr — M)

^S=S S~r ’    *%-ll    5~OTr

Oś walca B będzie się podnosić do góry, jeżeli M > > 2mgr.

Dwa jednorodne krążki o promieniach r i masach m j owi- PRZYKŁAD 15.7 męto nieważką nicią. Na jednym końcu nici zawieszono ciężar P =s mjg- Blok A jest umocowany na poziomej osi, blok B zaś, odwijając się z nici, opada w dół. Obliczyć przyspieszenie ciężarka, przyspieszenie osi 0\ bloku B oraz napięcia