Strona0086

86

Na podstawie rozwiązania (3.15) otrzymano dla ostatniego członu (3.14) wyrażenia:

±

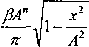
/3Aⁿ . --sm <o_Qt

K

(3.17)

Rezultat podstawiania ma znak minus, dlatego że rozpatrywany składnik znajduje się w jednej fazie z prędkością x. Przez podstawienie teraz wzorów (3.48) i (3.17) do równania (3.14) otrzymano równanie dla funkcji A(t) w postaci:

(3.18)

(3-19)

2^₀ +£r

ck u

lub po przekształceniu w postaci: kT₀ At

Rozwiązanie równania (3.19) nie daje dokładnego opisu procesu drgań tłumionych, ale pozwała łatwo znaleźć obwiednię: jeśli b =    , to:

kT_Q

-b-A*

AA

(U

(3.20)

- przy n = 0

.    . ad

A = A₀-bt = A₀--±_r kT₀

- przy n -1

^ai^ł

A = Ąe-^b‘ = Ąe ^k'^T° - przy n-2 j- Ą) __ Ą>

1 + bAftt | GCAąt

kT₀