265 (15)

530 20. Elementy analizy macierzowej obwodów

Na podstawie wzoru Sylvestera otrzymujemy

530 20. Elementy analizy macierzowej obwodów

exp

I 2 3 2

wobec tego

cz> li

= e^;-^,'F(/.₁) + e^/'²'F(ż₂) =

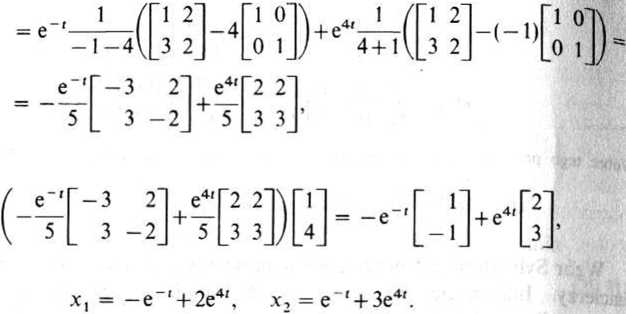
20.7. Rozwiązanie niejednorodnego równania stanu

20.7.1. Rozwiązanie ogólne

Wyznaczymy rozwiązanie równania stanu

dx

— = Ax + Be(t).    (20.35)

przy warunku początkowym x = x₀, gdy t = t₀. Przypuśćmy, że A jest macierzą kwadratową stopnia n. W punkcie 20.6 stwierdziliśmy, że rozwiązaniem jednorodnego równania stanu przy tym samym warunku początkowym jest wyrażenie

x = e^A(,_"’)x₀.    (20.36)

Rozpatrzymy macierz

<D(t —f₀) = e^A('-'^u,    (20.37)

będącą funkcją zmiennej l i noszącą nazwę macierzy tranzycyjnej. Macierz tranzycyj-na jest macierzą kwadratową, a jej wymiar jest taki sam jak macierzy kwadratowej A. Na podstawie wzoru (20.29) stwierdzamy, że macierz tranzycyjna spełnia równanie różniczkowe

^ = A<P(r-f₀),    (20.38)

a wartością początkową macierzy tranzycyjnej dla t = r_n jest <t>(0) = 1.

W celu rozwiązania równania stanu (20.35), zastosujemy metodę uzmiennienia

_stalej W związku z tym rozwiązanie tego równania przedstawimy w postaci

x = <D(r-r₀)C(r),    (20.39)

_g(jzie C(r) jest zależnym od czasu wektorem o n składowych. Różniczkując zależność (20.39) względem czasu, otrzymujemy

dx dO    dC(t)

a stąd po uwzględnieniu wzoru (20.38) mamy

dx    dC(t)

— = AO>(r-r₀)C(r) + <l>(r-t₀)—,

cz\ li

dx

dr

Ax + <t>(r-r₀)

dC(t) dr ’

z uwagi na zależność (20.39). Porównując otrzymane równanie z równaniem stanu (20.35). znajdujemy

dC(Q

dr

O(f-f₀)

= Be(r),

a stąd

dC(0

dr

= <D ¹ (r—r₀)Be(r),

przy czym <J> ^l(l-t₀) = e ^A" '^0|, wobec tego

C(r) = Ci + J d)^_,(T-r₀)Be(T)dT,

<0

gdzie stała całkowania C, jest stałym wektorem.

Podstawienie wyznaczonego wektora C(r) do wzoru (20.39) daje

x = <D(t-t₀)C₁ + j cD(r — to)⁴¹*^-Ł(^T —r₀)Be(r)dT,

to

a stąd

X = ®(r —r₀)C, + }<t>(r-T)Be(i)dT,    (20.40)

to

bowiem

®(_f__fo)®->(_T_,₀) = _eA« ,₀)_e-A(t-»o) _{= e}A(r-«) ₌ ®„__t)₅

zgodnie z określeniem macierzy tranzycyjnej (por. wzór (20.37)).