263 (16)

526 20. Elementy analizy macierzowej obwodów

Równania te można przedstawić w postaci macierzowej

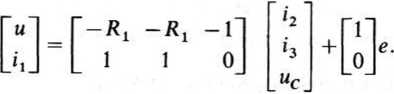
Wielkości u, i, można traktować jako odpowiedź układu; wektor [u, ij⁷ jest zatem wektorem odpowiedzi.

W ogólnym przypadku wektor odpowiedzi jest macierzą kolumnową, której elementami są odpowiedzi układu, czyli wielkości będące celem obliczeń. Na podstawie rozpatrywanego przykładu wnioskujemy, że wektor odpowiedzi, oznaczany symbolem y, można przedstawić w ogólnej postaci

y(0 = Cx(r)+De(r),    (20.24)

gdzie C i D są macierzami prostokątnymi. W przypadku stacjonarnych obwodów liniowych o parametrach skupionych elementy obu tych macierzy są stałymi.

Gdy badany obwód — ogólnie układ — ma n wejść (czyli n wymuszeń) i m wyjść (czyli m odpowiedzi), jak na rys. 1.1, wówczas wektor stanu jest n-wymiarowy, a wektor odpowiedzi jest m-wymiarowy.

20.6. Jednorodne równanie stanu

20.6.1. Rozwiązanie jednorodnego równania stanu

Jednorodnym równaniem stanu nazywamy równanie o postaci

dx

^ = Ax,    (20.25)

gdzie x jest wektorem stanu (20.22), zaś A jest macierzą kwadratową

	«n	^a12 '
A =	^a 21	°22 •	■■ 4>„
	-4u	4,2 ‘	'• 4* -

Zakładamy, że elementy macierzy A są wielkościami stałymi, niezależnymi od czasu. Jednorodne równanie stanu otrzymuje się z równania stanu (20.23), gdy wektor wymuszeń równa się zeru. Jednorodne równanie stanu w postaci rozwiniętej przedstawia układ n równań różniczkowych pierwszego rzędu:

dx₂

.    = ^21^1 "b ^a22*2 "b "b®2>i*n>

= a_n,x, +a„₂x₂+ ... +a_nnx_B.

Niech x₀ oznacza wartość początkową wektora stanu, tzn. wartość tego wektora w chwili t — t₀. Udowodnimy, że rozwiązaniem jednorodnego równania stanu jest

x = e^x<'~'^0,x₀,    (20.26)

gdzie /'(A) = _e^A<r_,°* jest funkcją macierzy kwadratowej A, którą określa się za pomocą szeregu nieskończonego

_eA(t-.o) ₌ 1 + L^_A + ⁽iZ^A² + ^^!A³ + ...+^^A* + ... (20.27) 1!    2!    3!    k\

Omawiana funkcja jest macierzą o takim samym wymiarze jak macierz A i istnieje dla dowolnej macierzy kwadratowej A.

Pochodną wyrażenia (20.26) względem t przedstawia wzór

dx

df

—    -Wlv

"dt^{L J} °’

(20.28)

bowiem x₀ jest wielkością stałą. Różniczkując szereg (20.27) wyraz po wyrazie, znajdujemy

\k- i

Ar_eA«-ton _ _A , [_^_A2 ₊ ^_*^_A³+    + -_a*

_dfLe j-A+ _{] A +    ₂, A +...+ _{k__iy

A* + ...=

= A

₁₊^A ₊

(t-t o)² 2!

A² + ...+

u-t₀rⁱ

(Ac- 1)! ‘

ik-i

czyli

iL[_eA«-'o>] _{= Ae}A(I-!o)    (20.29)

Podstawiając otrzymane wyrażenie do zależności (20.28), znajdujemy

— = _AeA"-‘<>)x₀,    (20.30)

df

skąd otrzymuje się równanie (20.25) po uwzględnieniu wzoru (20.26). Oznacza to, że wyrażenie (20.26) spełnia jednorodne równanie stanu. Spełnienie warunku początkowego wynika natychmiast z podstawienia t = t₀ do wzoru (20.27), bowiem

e^A0 = 1.

Wyrażenie (20.26) będące rozwiązaniem jednorodnego równania stanu można