266 (19)

532

20. Elementy analizy macierzowej obwodów

W celu wyznaczenia wektora Cl5 podstawiamy t = r0 otrzymujemy x0 = O^O)^ = Ci, bowiem <f>(0) = 1. Zgodnie ze wzorem (20.40) mamy	do równania (20.40);
i X = O(r-r0)x0 + fO^-ijBe^dT,	(20.41)
• u czyli
x = e^A(' “^,0) x0 + J e^A" -Be(r)dr, to	(20.42)
Dla t„ = 0 otrzymujemy
x = e^A'x0 +je^A('“^r,Be(T)dt.	(20.43)

O

Wzory (20.41 H20.43) pozwalają wyznaczyć rozwiązanie równania stanu w zależności od macierzy tranzycyjnej.

Macierz tranzycyjna ma prostą interpretację. Gdy w układzie nie ma żadnych wymuszeń (e = 0), wówczas — jak to wynika ze wzoru (20.41) — macierz tranzycyjna charakteryzuje przejście od stanu początkowego w chwili f₀, opisanego przez wektor x₀, do stanu w chwili t, opisanego przez wektor x(f) = <t>(f — f₀)x₀.

Przykład 1. Rozwiążemy równanie stanu

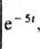
d

d/ przyjmując warunek początkowy x₀ =

Macierz tranzycyjna rozpatrywanego równania została wyznaczona w p. 20.6.3. a mianowicie:

exp<

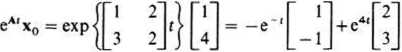
Wyrażenie

występujące we wzorze (20.43) zostało obliczone również we wspomnianym przykładzie. Zgodnie z zależnością (20.43), rozwiązanie rozpatrywanego równania stanu wyraża się wzorem:

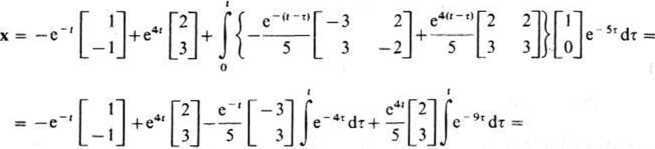
,uid po wykonaniu prostych obliczeń, otrzymujemy

=    ⁹²l ₊ -^[-³⁵le-⁵'

20 L '⁷J 45L138J 180|_ J5J

20.7.2. Macierz tranzycyjna

Z rozważań zawartych w p. 20.7.1 wynika, że macierz tranzycyjna

<D(r) = e^A'    (20.44)

spełnia równanie różniczkowe

(20.45)

= A<D(r)

d<D

dt

przy warunku początkowym <D(0) = 1. Przekształcając powyższe równanie za pomocą transformacji Laplace’a, mamy

<Ks)-

0(0)“

= A fc(s).

gdzie <t»(.s) oznacza transformatę macierzy tranzycyjnej <t>(r); wobec tego |.vl - A)<I>(s) = 1, a stąd znajdujemy

$(s) = (sl-A)"¹    (20.46)

czyli

<t»(/) = e^A' = 2Z"¹ {(sl — A)^-1}.    (20.47)

Otrzymaliśmy prosty wzór dla macierzy tranzycyjnej. Okazuje się jednak, że obliczanie macierzy tranzycyjnej za pomocą wzoru (20.47) jest dość uciążliwe.

Przykład 2. Wyznaczymy za pomocą wzoru (20.47) macierz tranzycyjną dla

sl - A

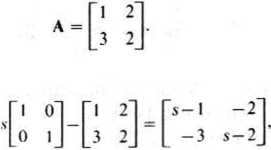
s- I -3

Mamy wtedy

wobec tego wyznacznik tej macierzy

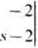
= (s+l)(s —4)

dct(xl — A)