258 (18)

516 20. Elementy analizy macierzowej obwodów

AB^rI₀ = 0. Równanie to jest spełnione dla dowolnych prądów Oczkowych,

^art-»■    E

Wprowadzony wzór podaje związek między macierzami łączącymi.

W celu otrzymania drugiej zależności między macierzami łączącymi, dokona^ transpozycji obu stron równania macierzowego (20.6); mamy wówczas (AB¹)⁷ _Ł q bowiem transpozycja macierzy zerowej jest macierzą zerową.

Obliczamy transpozycję iloczynu dwóch macierzy i otrzymujemy

BA^r = 0,    (20.7)

bowiem po dwukrotnej transpozycji macierzy B otrzymuje się macierz B.

Przykład 5. Wykorzystując macierze łączące z przykładów 1 i 3 dla obwodu z rys. 20.1, oiatny (zgodnie z wzorem (20.6)):

					1	0	0
					0	0	-1
1 0-1	1	0	0
					0	1	0
-1-1 0	0	-1	0
					-1	1	0
.011	0	0	-1
					-1	0	1
					0	1	-1

0 0 0 0 0 0 0 0 0

20.2.5. Twierdzenie Tellegena

Rozpatrzmy obwód mający n gałęzi i ot węzłów. Niech i oraz u oznaczają odpowiednio wektory prądów gałęziowych i napięć gałęziowych (dla wartości chwilowych). Wyrażenie

u^ri = ^ "jij 7=1

przedstawia sumę mocy chwilowych w obwodzie. Podstawiając wzór na transformację węzłową u^T = A^ru₀ i uwzględniając I prawo Kirchhoffa w postaci macierzowej Ai = 0, mamy

u^Ti = (A^ru₀)^ri = Uq Ai = 0.

Wzór ten wyraża

Twierdzenie (Tellegena). Suma mocy chwilowych obwodu jest równa zeru. Omawiane twierdzenie można uogólnić. Rozpatrzmy dwa obwody N i ^ których grafy są takie same, lecz obwody różnią się elementami zawartym* w odpowiadających sobie gałęziach. Załóżmy, że gałęzie i węzły obu grafów są jednakowo ponumerowane, a zwroty prądów w odpowiadających sobie gałęziach są

_takie same. Rozpatrzymy iloczyn wektora u^r dotyczącego obwodu N i wektora

i dotyczącego obwodu Ń:

U^Ti = X Ujlj, j= i

który obecnie nie ma interpretacji fizycznej, gdyż prądy i napięcia należą do różnych obwodów. W podobny sposób — jak poprzednio — znajdujemy

u⁷1 = (A^ru₀)^ri = Uq Ai = 0,

bowiem A = A, wobec tego Ai = Ai = 0, zgodnie z I prawem Kirchhoffa w postaci macierzowej. Otrzymany wzór wyraża uogólnione twierdzenie Tellegena. Czytelnikowi pozostawia się do wyprowadzenia wzór

u^ri = i^ru = u^ri = i⁷ u = 0

przedstawiający różne warianty uogólnionego twierdzenia Tellegena.

Twierdzenie Tellegena znajduje zastosowanie przy analizie obwodów elektronicznych [11],

20.3. Macierze impedancji i admitancji gałęziowych

20.3.1. Macierz impedancji gałęziowych

W dalszym ciągu rozpatrywać będziemy obwody o zerowych warunkach początkowych; wobec tego przyjmujemy, że w chwili t = 0 równe są zeru prądy we wszystkich cewkach i napięcia na wszystkich kondensatorach.

Na wstępie zajmiemy się obwodami nie zawierającymi ani cewek magnetycznie sprzężonych, ani źródeł prądu, ani też źródeł sterowanych. Omawiane obecnie obwody zasilane będą wyłącznie przez źródła napięcia. Gdyby obwód zawierał źródła prądu, należałoby je zastąpić równoważnymi źródłami napięcia.

/_y(s i

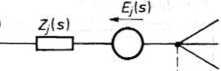
Rys. 20.2. Gałąź obwodu elektrycznego

Każdą gałąź obwodu spełniającego założenia powyższe można przedstawić w postaci szeregowego połączenia impedancji gałęziowej Zj(s) oraz idealnego źródła napięcia o napięciu źródłowym £_y(s) (rys. 20.2).

Napięcie gałęziowe rozpatrywanej gałęzi wynosi

(20.8)

Uj(s) = Zj(s) łj{s)- E/s),