259 (14)

518 20. Elementy analizy macierzowej obwodów

gdzie Ij(s) jest prądem gałęziowym. Dla obwodu zawierającego n gałęzi oznaczonych ł, 2,..., n można napisać n równań typu (20.8), wobec tego j = 1, 2, n w tym równaniu. Jeżeli w pewnej gałęzi k nie ma źródła napięcia, to należy wówczas przyjąć E_k(s) = 0. Zbiór wszystkich równań dla napięć gałęziowych obwodu można przedstawić w postaci macierzowej

U = ZI —E,    (20.9)

gdzie U jest wektorem napięć gałęziowych, a I — wektorem prądów gałęziowych.

Przy przyjętych założeniach, macierz Z w równaniu (20.9) jest diagonalna, a elementami przekątnej głównej są impedancje poszczególnych gałęzi:

-Z,(s)    0 *

(20.10)

Z₂(s)

. 0    Z_n(s)_

Macierz Z nazywa się macierzą impedancji gałęziowych.

Macierz E jest kolumnowa, a jej elementami są napięcia źródłowe występujące w poszczególnych gałęziach, czyli

E =

Ei(s)

E₂(s)

(20.11)

W)

Elementy macierzy E mają znak plus, gdy zwrot napięcia źródłowego jest niezgodny z prądem gałęziowym (jak na rys. 20.2), a znak minus — w przypadku przeciwnym. Gdy w pewnej gałęzi nie ma źródła napięcia, wówczas odpowiedni element macierzy E jest równy zeru.

E, Isl

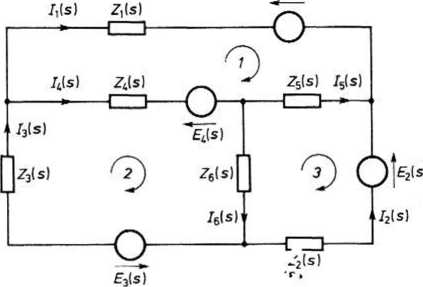
Rys. 20.3. Przykład obwodu elektrycznego

Przykład 1. Dla obwodu przedstawionego na rys. 20.3 macierz impedancji gałęziowych

Z,(s)

Z₂(s)    0

7 _    (*)

ZJs)

Z_s[s)

0    Z₆(s)_

a ponadto

£i(s)'

~E₂(s)

E₃(s)

EJs) '

0

0

Gdy obwód zawiera cewki magnetycznie sprzężone lub źródła sterowane, wówczas wzór (20.9) jest słuszny, jednakże macierz kwadratowa Z nie jest diagonalna. Macierz tę można ułożyć na podstawie równań dla poszczególnych napięć

gałęziowych.

i-h

Rys, 20.4. Obwód zawierający cewki magnetycznie sprzężone oraz źródło sterowane

Przykład 2. Dla obwodu podanego na rys. 20.4 otrzymujemy następujące równania dla napięć

gałęziowych:

U,(s) = [Z, (s) + sL, ] /, (s) + sM / ₃(s) - £(s),

U₂(s) = Z₂(s)I₂(s)—aI₃(s),

U₃(s) = sM/_t(s) + pZ₂(s)/₂(s) + [Z₃(s) + sL₃]l₃(s),

wobec tego macierz impcdancji gałęziowych przybiera postać

Z,(s) + sL, 0 sM

Z =

0    Z₂(s) —a

sM    pZ₂(s) Z₃(s) + sL₃