262 (18)

524 20. Elementy analizy macierzowej obwodów

20.5. Równania stanu

W celu otrzymania równań stanu obwodu elektrycznego rozpatrujemy prądy i_lt we wszystkich cewkach oraz napięcia u_ci, u_C2,... na wszystkich kondensatorach zawartych w obwodzie przy założeniu, że każda gałąź obwodu zawiera poza opornikiem co najwyżej jedną cewkę i jeden kondensator. Prądy i_t, i₂,... we wszystkich cewkach i napięcia u_ci, w_c2,... na wszystkich kondensatorach obwodu noszą nazwę zmiennych stanu. Oznacza to, że liczba zmiennych stanu obwodu jest równa liczbie wszystkich cewek i kondensatorów zawartych w obwodzie. Zmienne stanu określają stan obwodu, bowiem na ich podstawie można określić prąd w każdej gałęzi oraz napięcie między każdymi dwoma punktami obwodu. Tłumaczy to nazwę zmiennych stanu.

W celu otrzymania równań stanu układamy równania na podstawie I i II prawa Kirchhoffa. Następnie eliminujemy z tych równań wszystkie prądy nie będące

zmiennymi stanu i przy zastosowaniu zależności o ogólnej postaci i = dla

dt

prądu płynącego w gałęzi zawierającej kondensator, wyznaczamy pochodne zmiennych stanu w zależności od tych zmiennych oraz od napięć i prądów źródłowych.

u

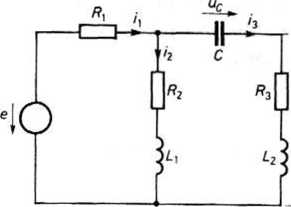
Rys. 20.6. Przykład obwodu elektrycznego

Sposób postępowania przedstawimy na przykładzie obwodu z rys. 20.6. Zmiennymi stanu w tym obwodzie są i₂, i₃ oraz u_c. Na podstawie I i II prawa Kirchhoffa otrzymuje się równania:

di.

/?_t ii + u_c +/?₃/j + L₂-^y = e,

' 2+*3-

Podstawiając i, =i₂ + i₃ do pierwszych dwóch równań, znajdujemy:

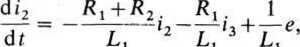
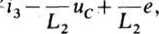
di₃    R j    R, + R,

df    L₂² L₂

_a trzecie równanie przybiera postać

du_c 1 .

~d7 ⁼ Ć'³‘

Są to równania stanu rozpatrywanego obwodu.

Otrzymane równania stanu można przedstawić w postaci macierzowej:

R, +/?2	Rt	0				■ 1'
	U			i 2		Lt
Rl	Ri +R3	1			+	1
1 1	l2 1	^2		^ł3 _«c_		Li
0		0				0
	c

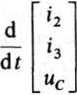
Przypuśćmy, że obwód elektryczny zawiera kilka źródeł energii. Niech x,. x₂,..., x„ oznaczają zmienne stanu rozpatrywanego obwodu. Macierz kolumnowa

(20.22)

nazywa się wektorem stanu. Elementami wektora stanu są zmienne stanu. Wektorem stanu w przypadku obwodu z rys. 20.6 jest x = [i₂, i₃, u_c]^T, gdzie górny indeks T oznacza transpozycję.

Wektorem wymuszeń nazywamy macierz kolumnową, której elementami są napięcia źródłowe e₂, e₂, ..., e_k oraz prądy źródłowe j_v,j₂,wszystkich źródeł napięcia i prądu zawartych w obwodzie. Wektor wymuszeń oznaczamy symbolem e. Ogólną postacią wektora wymuszeń jest zatem e = [e₂, e₂,..., e_k,j_l,j₂,...,j_m]^T. Wektor wymuszeń dla obwodu z rys. 20.6 zawiera tylko jeden element e. Równania stanu można ogólnie przedstawić w postaci macierzowej

(20.23)

— = Ax(r)-f Be(r), dr

gdzie A jest macierzą kwadratową, natomiast B — macierzą prostokątną. W przypadku stacjonarnych obwodów liniowych o parametrach skupionych elementy obu tych macierzy są stałymi.

Znajomość zmiennych stanu umożliwia wyznaczenie dowolnych prądów i napięć w obwodzie. Przypuśćmy, że w przypadku obwodu z rys. 20.6 celem naszych obliczeń są napięcie u oraz prąd mamy

ii = h + h^

_u = g-R^-Uc = _e-R_ii₂-R_li₃-u_c.