256 (19)

512 20. Elementy analizy macierzowej obwodów

Pierwsze prawo KirchhofTa przybiera zatem postać

		/,(*)
t - o o 7 o
o 0 1 o		his)
0 1 10 0-1		IJs)
		/5(s)

a stąd po wykonaniu mnożenia, mamy

- /,(s) -l3(s) +IJsY		'0'
-/l(s) -/2(s) ~/5(s)	=	0
. /2(s) + l3(s) —/6(s)		.0

Powyższe wyrażenie przedstawia równania otrzymane na podstawie I prawa KirchhofTa dla węzłów /, 3 i 4, co można sprawdzić bezpośrednio.

Niech U'i(s), i = 1, 2,..., p, przy czym p = a—1 oznacza transformatę napięcia węzłowego, które jest równe potencjałowi węzła niezależnego względem węzła odniesienia (por. p. 5.5). Wszystkie napięcia węzłowe przedstawiamy w postaci macierzy kolumnowej

[U\(s)l

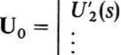
tWJ

zawierającej p = a — 1 elementów i nazywanej wektorem lub macierzą napięć węzłowych. Napięcia gałęziowe są równe odpowiednim napięciom węzłowym pomnożonym przez 1 lub -1, albo różnicy odpowiednich napięć węzłowych.

Wektor napięć gałęziowych U jest związany z wektorem napięć węzłowych U₀ za pomocą wzoru

U = A^TU₀,    (20.3)

gdzie A^r jest transponowaną macierzą łączącą węzłową. Wzór (20.3) można traktować jako przekształcenie wektora napięć węzłowych na wektor napięć gałęziowych; wzór ten nosi nazwę transformacji węzłowej.

Przykład 2. Transformację węzłową dla obwodu z rys. 20.1 przedstawia wzór

		1-1 o’
U2(s)		0 -1 1
U3(s)		-1 0 1
UJs)		1 0 0
U s(s)		0-1 0
U„(s)		0 0-1

U\(s)'

U'As)

U\(s)_

przy założeniu, że węzłami niezależnymi są węzły i, 3, 4. Po wykonaniu mnożenia znajdujemy

		U\(s)-U'3(s)
t/2(s)		— U'3(s)+1/4(5)
		-t/j(s)+t/i(s)
1/4IS)		t/j(i)
Vs(s)		-U'3(s)
Ub(s)		— U*(s)

Stwierdzamy zatem, że napięcia gałęziowe są równe różnicy odpowiednich napięć węzłowych albo pomnożonym przez 1 lub — 1 odpowiednim napięciom węzłowym. Otrzymany wynik można sprawdzić

bezpośrednio na podstawie obwodu z rys. 20.1

Jest rzeczą oczywistą, że wzory (20.2) i (20.3) dotyczące I prawa KirchhofTa w postaci macierzowej i transmitancji węzłowej są również prawdziwe dla wartości

chwilowych prądów i napięć.

20.2.3. II prawo KirchhofTa

Dla obwodu zawierającego n gałęzi i a węzłów można na podstawie II prawa Kirchhoffa ułożyć m = n —a + 1 równań liniowo niezależnych dla wszystkich oczek niezależnych. Oczka niezależne obwodu oznaczamy liczbami 1, 2oraz przyjmujemy jednakowy dla wszystkich oczek zwrot obiegu; w dalszych rozważaniach przyjmować będziemy, że zwrot obiegu jest zawsze zgodny z ruchem wskazówek zegara.

Rozpatrujemy macierz prostokątną o wymiarze mxn

B = [fcy],

przy czym i = 1,2m orazj = 1,2..... n. Liczba wierszy tej macierzy odpowiada

liczbie oczek niezależnych, a liczba kolumn — liczbie gałęzi obwodu. Elementy macierzy B określamy w sposób następujący:

b_tJ = 1, gdy oczko i zawiera gałąź j, a zwrot prądu w tej gałęzi jest zgodny z ruchem wskazówek zegara;

bu = — 1, gdy oczko i zawiera gałąź j, a zwrot prądu w tej gałęzi jest przeciwny względem ruchu wskazówek zegara;

bij = 0, gdy oczko i nie zawiera gałęzi j.

Macierz B nazywa się macierzą łączącą oczkową lub macierzą incydencji oczkową\ układa się ją według schematu:

Gałęzie Oczka	1, 2, •••,«
1		^bM ^bl2 - ^bln
2		^b21 b22 ■■■ b2n
m		^bm\ bm2 ••• bmn