Strona0102

102

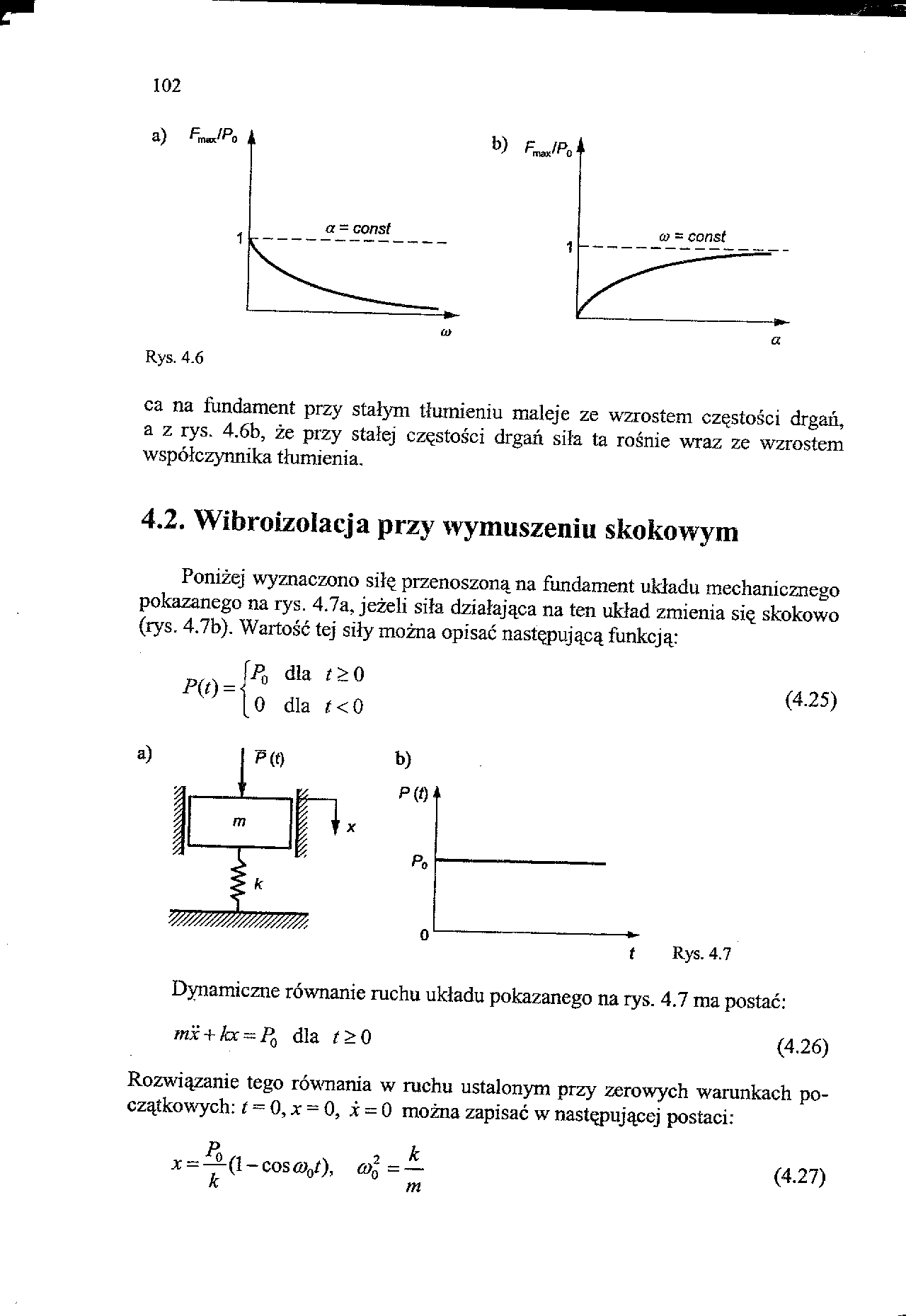
Rys. 4.6

ca na fundament przy stałym tłumieniu maleje ze wzrostem częstości drgań, a z rys. 4.6b, że przy stałej częstości drgań siła ta rośnie wraz ze wzrostem współczynnika tłumienia.

4.2. Wibroizolacja przy wymuszeniu skokowym

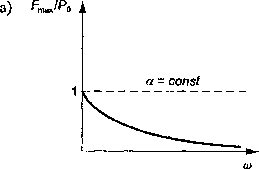
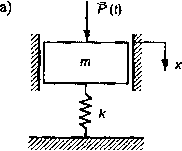
Poniżej wyznaczono siłę przenoszoną na fundament układu mechanicznego pokazanego na rys. 4.7a, jeżeli siła działająca na ten układ zmienia się skokowo (rys. 4.7b). Wartość tej siły można opisać następującą funkcją:

(4.25)

JR dla t>0

^v [0 dla t< 0

b)

P(t)n

Po -

0-^

t Rys. 4.7

Dynamiczne równanie ruchu układu pokazanego na rys. 4.7 ma postać:

mx + kx~P_Q dla t> 0    (4.26)

Rozwiązanie tego równania w ruchu ustalonym przy zerowych warunkach początkowych: t - 0, * = 0, x = 0 można zapisać w następującej postaci:

(4.27)

P    Ję

x -—(1 - cos 0)_Qi), (Ą = — k    m