0000018 2

d u o 1 n y r H* dla hipergrafu H ■ <*X,Ł> ; C- |Ej.....E^j.

Hlporgraf dualny H* • <E,\> okreólony jost następująco: E •

• {cj.....o_m J . \» {x......X_n] . Wierzchołki o odpowiadają

hiporkrawędziOD Lj. natomiast podzbiory X^ okroolona oę następująco

^xi ■{•j ■ *»^{€ e}3)

Przykład 2.4

woZey jako H • <X, L > hipergraf symetryczny z przykła -du 2.2. który jaat hlpergrafom prostye. Binarna macierz incy-doncjl tego hiporgrafu ca postać (hiporgraf jaat przedstawiony na rys.2.2)

	^E1	^E2	^E3	^E4	^E5	^E6	E
1	1	0	0	1	0	0	0
2	0	1	0	0	0	0	0
3	0	0	1	0	0	0	0
4	0	1	0	0	0	0	0
5	1	0	0	0	0	0	1
6	0	0	0	1	1	0	0
7	0	0	0	1	0	1	0
e	0	0	1	0	0	1	0
9	0	0	0	0	0	1	1
10	0	0	0	0	0	0	1

Binarna macierz lncydencji hipergrafu dualnogo H* Jest równe A^T 1 e® postać

	^X1	^X2	^X3	*4	^x5	^X6	^X7	^X6	^X9	o X
1	' 1	0	0	0	1	0	0	0	0	0
2	0	1	0	1	0	0	0	0	0	0
	0	0	1	0	0	0	0	1	0	0
A(H* ) • 4	1	0	0	0	0	1	1	0	0	0
5	0	0	0	0	0	1	0	0	0	0
6	0	0	0	0	0	0	1	1	1	0
7	0	0	0	0	1	0	0	0	1	1

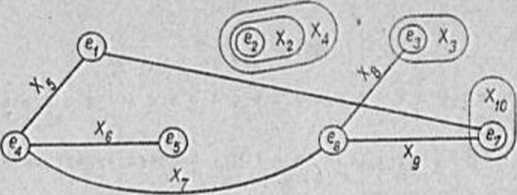
Hipergraf dualny H* • <E.X> J®*« przedetawiony na rys.2.«. Hipergraf H* . który tai jest hiporgrafom symetryczny*, w od -różnieniu od H ma jest Jut hiporgrofcm prosty*. poniowoZ jogo X_i nio co róZne (X₂ ■ X₄).

Rya.2.4

Widać wyróżnia, że warunek dla hiperQrofu prostego UE,»X jaat warunkiem koniecznym i wyaterczajocym dla lotnienia hipor-grafu dualnego.

2.2.2. Macierze przyległości

Mociarz przyległości wierzchołków:

R* [^rij] n*n ^{; n} "    ®*^ci#rz eymetryczna

ilości gałęzi (hiporgołęzi) incydontnych jednocześnie z wierzchołkiem x_ł oraz Xy gdy x_i#Xj e« przyległa

O gdy *_A nie jaat przyległy do x^

Olo grafu C ■ <X,U,P>

r

u e u :

Xj ,u>€ P v <x_J,x₁.u> € p}|

Wierzchołek w grofie jaat przyległy do eiobie wtedy 1 tylko wtedy, gdy jeat incydontny z pętlo.

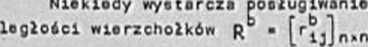
alf binarno maciorzę przy-

35